تمارين عامة على الوحدة الرابعة (المساحات)
١) في الشكل المقابل: // ، س، ص س ء هـ ص مستطيل، // .
أولاً: أوجد مساحة الشكل أ ب هـ ء.
مساحة المستطيل س ء هـ ص = مساحة الشكل أ ب هـ ء
لأن أ ص // ء هـ
وأيضاً ء هـ قاعدة مشتركة
مساحة المستطيل س ء هـ ص = ٢٤ × ١٢ = ٢٨٨سم٢
مساحة الشكل أ ب هـ ء = ٢٨٨سم٢
ثانياً: إذاً كان أ ء = ٣٠ سم فأوجد طول العمود النازل من ب على .
مساحة الشكل أ ب هـ ء = طول القاعدة × الارتفاع
٢٨٨ = ٣٠ × الارتفاع
الارتفاع = ٢٨٨ ÷ ٣ = = ٩,٦ سم.
٢) في الشكل المقابل: ل م ن هـ متوازي أضلاع. برهن أن: مساحة المثلث ل هـ و + مساحة المثلث م و ن = مساحة المثلث ل هـ م.
ل م ن هـ متوازي أضلاع والمثلث ل هـ م محصور بين مستقيمين متوازيين ل هـ، م ن وأيضاً ل هـ قاعدة مشتركة
مساحة المثلث ل هـ م = مساحة متوازي الأضلاع ل م ن هـ
المثلثين ل هـ و، م و ن لهم قاعدة مشتركة هـ ن
المثلث ل هـ و قاعدته ل م
ل م = هـ ن
القاعدتان متساويتان المثلثان ل هـ و، م و ن
ل هـ و تنحصر بين مستقيمين متوازيين ل م، و ن
مساحة المثلث ل هـ و + مساحة المثلث م ون = مساحة المثلث ل هـ م
٣) أ ب جـ ء، ب هـ جـ ء متوازيا أضلاع = {م}. برهن أن: مساحة المثلث أ ب ء = مساحة المثلث م هـ جـ
المثلث أ ب ء ومتوازي الأضلاع أ ب جـ ء لهم قاعدة مشتركة أ ء وهما بين مستقيمين متوازيين أ ء، ب هـ
مساحة المثلث أ ب ء = مساحة متوازي الأضلاع أ ب جـ ء
المثلث م هـ جـ، ومتوازي الأضلاع ب هـ جـ ء لهم قاعدة مشتركة هـ جـ وتنحصر بين مستقيمين متوازيين ب ء، هـ جـ
مساحة المثلث م هـ جـ = مساحة متوازي الأضلاع ب هـ جـ ء
مساحة متوازي الأضلاع أ ب جـ ء = مساحة متوازي الأضلاع ب هـ جـ ء
إذاً مساحة المثلث أ ب ء = مساحة المثلث م هـ جـ
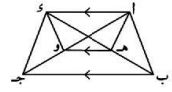
٤) في الشكل المقابل: // // برهن أن: مساحة المثلث أ ب هـ = مساحة المثلث ء جـ و.
// مساحة المثلث أ ب ء = مساحة المثلث أ جـ ء لها القاعدة
// مساحة المثلث أ هـ ء = مساحة المثلث أ و ء لها القاعدة
بطرح ١) من ٢ مساحة المثلث أ ب هـ = مساحة المثلث ء و جـ
٥) في الشكل المقابل: أ ب = أ جـ. ،
أولاً: برهن أن //
ثانياً: مساحة المثلث أ ء ب = مساحة أ هـ جـ
٦) في الشكل المقابل: // برهن أن: مساحة المثلث أ ب م = مساحة المثلث ء م جـ، وإذا كانت مساحة المثلث م ب جـ = ٢٠سم٢، ومساحة المثلث أ م ب = ٣ أمثال مساحة المثلث م ب جـ، احسب مساحة المستطيل المنشأ على بحيث تقع قاعدته الأخرى على
// مساحة المثلث أ ب جـ = مساحة المثلث ء ب جـ
بطرح المثلث ب م جـ من الطرفين
فإن مساحة المثلث أ ب م = مساحة المثلث أ جـ م
مساحة المستطيل = ٨٠ × ٢ = ١٦٠سم٢

.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)