الدرس الأول: النسب المثلثية الأساسية للزاوية الحادة

١) في الشكل المقابل: أكمل

في المثلث س ع ص قائم في ع

ص س = = ٥ سم.

أ) جا س = ............

جا س =

ب) جتا س = ............

جتا س =

جـ) ظا س = ............

ظا س =

د) جتا ص = ............

جتا ص =

هـ) ظا ص = ............

ظا ص =

و) جا ص = ............

جا ص =

٢) إذا كانت النسبة بين قياسي زاويتين متتامتين كنسبة ٣ : ٥ فأوجد مقدار كل منهما بالقياس الستيني.

الأولى : الثانية : المجموع

٣ : ٥ : ٨

س : ص : ٩٠

س = = ٠ً ٤٥َ ٣٣°

ص = = ٠ً ١٥َ ٥٦°

٣) إذا كانت النسبة بين قياسي زاويتين متكاملتين كنسبة ٣ : ٥ فأوجد مقدار كل منهما بالقياس الستيني.

الأولى : الثانية : المجموع

٣ : ٥ : ٨

س : ص : ١٨٠

س = = ٠ ً ٣٠ َ ٦٧°

ص = = ٠ ً ٨٠ َ ١١٢°

٤) إذا كنت النسبة بين قياسات زوايا كنسبة ٣ : ٤ : ٧ فأوجد القياس الستيني لكل زاوية من زواياه.

الأولى : الثانية : الثالثة : المجموع

٣ : ٤ : ٧ : ١٤

س : ص : ع : ١٨٠

س = = ١٧ ً ٣٤ َ ٣٨°

ص = = ٤٣ ً ٢٥ َ ٥١°

ع = = ٠ ً ٠ َ ٩٠°

٥) أ ب جـ مثلث قائم الزاوية في ب فيه أ ب = ٨ سم، ب جـ = ١٥ سم، اكتب ما تساويه كل من النسب المثلثية الآتية: جا حـ، جتا أ، جتا حـ، ظا حـ.

في المثلث أ ب جـ قائم في ب

أ جـ = = ١٧

جا جـ =

جتا أ =

جتا جـ =

ظا جـ = =

٦) أ ب جـ مثلث قائم الزاوية في ب، فإذا كان ٢ أ ب = أ جـ فأوجد النسب المثلثية الأساسية للزاوية جـ.

٢ أ ب = أ جـ

ب جـ = = ١

جا جـ =

جتا جـ = =

ظا جـ = =

٧) في الشكل المقابل: أ ب جـ مثلث ق ( أ) = ٩٠°، أ جـ = ١٥ سم، أ ب = ٢٠ سم

أثبت أن: جتا جـ جتا ب - جا جـ جا ب = صفر

في المثلث أ ب جـ قائم في أ

ب جـ = ٢٥ سم.

جتا جـ جتا ب - جا جـ جا ب =

= ٠

٨) س ص ع مثلث قائم الزاوية في ص فيه س ص = ٥ سم، س ع = ١٣ سم

أوجد قيمة:

في المثلث س ص ع قائم في ص

ص ع = = ١٢ سم

أ) ظا س + ظا ع

ظا س + ظا ع =

ب) جتا س جتا ع - جا س جا ع

جتا س جتا ع - جا س جا ع = = صفر.

جـ) جا س جتا ع + جتا س جا ع

جا س جتا ع + جتا س جا ع = = ١

٩) س ص ع مثلث قائم الزاوية في ع، س ع = ٧ سم، س ص = ٢٥ سم، أوجد قيمة كل من:

في المثلث س ص ع قائم في ع

ع ص = = ٢٤ سم

أ) ظا س × ظا ص

ظا س × ظا ص = = ١

ب) جا^٢ س + جا^٢ ص

جا^٢ س + جا^٢ ص = ()^٢ + ()^٢ = = ١

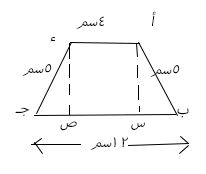
١٠) أ ب جـ ء شبه منحرف متساوي الساقين فيه // ، أ ء = ٤سم، أ ب = ٥ سم، ب جـ = ١٢ سم

أثبت أن: = ٢

العمل نرسم ،

الحل: ،

// ، //

إذاً الشكل أ س ص ء مستطيل

أ ء = س ص = ٤ سم، أ س = ء ص

أ س ب، ء ص جـ

أ ب = ء جـ

ق ( أ س ب) = ق ( ء ص جـ) = ٩٠°

أ س = ء ص

أ س ب ء ص جـ

وينتج من التطابق ب س = ص جـ = = ٤ سم.

أ س = = ٣ سم.

= = ٣

١١) أ ب جـ مثلث فيه أ ب = أ جـ = ١٠ سم، ب جـ = ١٢ سم، رسم ، = {ء}

أ ب = أ جـ،

ب ء = ء جـ = = ٦ سم.

من فيثاغورث أ ء = = ٨ سم.

أولاً: أوجد قيمة: جا ( جـ أ ء)، جتا ( جـ أ ء)، ظا ( جـ أ ء)

جتا ( جـ أ ء) =

جا ( جـ أ ء) =

ظا ( جـ أ ء) =

ثانياً: أثبت أن:

أ) جا^٢ جـ + جتا^٢ جـ = ١

جا^٢ جـ + جتا^٢ جـ = = ١

ب) جا ب + جتا جـ > ١

جا ب + جتا جـ = > ١