الدرس الثاني: ميل الخط المستقيم وتطبيقات حياتية
١) أكمل لتحصل على عبارة صحيحة:
أ) إذا كان أ (١، ٣)، ب (٢، ١) فإن ميل يساوي .....
م =
م = = -٢
ب) إذا كان (-١، ٥) يحقق العلاقة ٣س + ك ص = ٧ فإن ك = ......
٣س + ك ص = ٧
٣س + ك ص = ٧
٣ × -١ + ك × ٥ = ٧
-٣ + ٥ك = ٧
٥ ك = ٧ + ٣ = ١٠
ك = ٢
جـ) أي مستقيم يوازي محور السينات ميله = ......
صفر.
د) أي مستقيم يوازي محور الصادات ميله .......
غير معرف أو
هـ) إذا كانت أ، ب، جـ على استقامة واحدة فإن ميل = ميل .......
= ميل
٢) مع عصام ١٠ ورقات مالية فئة ٥ جنيهات، وأوراق مالية فئة ٢٠ جنيهاً، اشترى عصام من المركز التجاري بما قيمته ٥ جنيهاً، حدد الإمكانات المختلفة لدفع هذا المبلغ باستخدام الأوراق المالية التي معه، وأوجد العلاقة بين عدد كل منها ومثلها بيانياً.
فئة ٢٠ (ص)
فئة ٥ (س)
| س | ٩ | ٥ | ١ |
| ص | ١ | ٢ | ٣ |
٣) إذا كان ثمن طاولة كمبيوتر ١٠٠ جنيه وثمن الكرسي ٥٠ جنيهاً، فإذا باع المتجر في أحد الأسابيع بمبلغ ٥٠٠ جنيه، فما هي التوقعات الممثلة لعدد الطاولات التي باعها، وعدد الكراسي. مثل هذه العلاقة بيانياً؟
عدد طاولات الكمبيوتر س
عدد الكراسي ص
١٠٠س + ٥٠ص = ٥٠٠
| س | ٠ | ١ | ٢ | ٣ | ٤ | ٥ |
| ص | ١٠ | ٨ | ٦ | ٤ | ٢ | ٠ |
٤) في الشكل المقابل المثلث أ ب جـ أكمل باستخدام أحد الكلمات: (موجب أو سالب أو صفر أو غير معروف)
أ) ميل ......
سالب
ب) ميل .....
صفر
جـ) ميل .....
غير معرف
د) ميل .....
موجب.
٥) في الشكل المقابل: ل م ن مثلث قائم الزاوية في ل، ق () = ٤٥° فإذا كان ل (٣، ٢)، م (٧، ٢) أوجد إحداثي ن واحسب ميل .
ن = (٣، ٦)، (٧، ٢)
م ن =
م ن = = -١
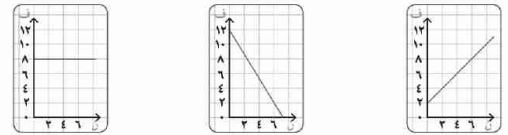
٦) كل من الأشكال التالية يوضح العلاقة بين المسافة ف (بالمتر) والزمن ن (بالثانية) لجسم. حدد موضع الجسم عند بدأ الحركة، وعند ن = ٦ ثوان، وأوجد ميل المستقيم في كل حالة (ماذا يمثل الميل؟).
الشكل الأول س = ٠ الميل = ٢
الشكل الثاني س = ٢، الميل = -٢
الشكل الثالث = الميل المستقيم يوازي محور السينات. المسافة ثابتة بالنسبة للزمن. الجسم ثابت)

.JPG)
.JPG)
.JPG)
.JPG)
.JPG)