تمارين عامة على الوحدة الثالثة

(١) ضع علامة (✔) أمام العبارة الصحيحة، وعلامة (×) أمام العبارة الخطأ مع تصويب الخطأ إن وجد:

أ) البعد بين النقطتين (٣، ٥)، (-٢، ٥) = ٥ وحدة طول (✔)

$\left|\mathrm{٣} - (-\mathrm{٢})\right|$ = $\left|\mathrm{٣} + \mathrm{٢}\right|$ = ٥ وحدة

✔

ب) يتحدد الانتقال في مستوى بمقداره واتجاهه (✔)

✔

جـ) صورة النقطة (-١، ٤) بالانتقال (١، -٣) هي النقطة (٢، ٧) (×)

(-١ +١، ٤ -٣) = (٠، ١)

(×)

د) مساحة دائرة طول نصف قطرها ٧ سم = ٧ $\mathrm{\pi }$ سم^٢ (✔)

مساحة الدائرة = $\mathrm{\pi }$ نق^٢

= $\mathrm{\pi }$ × ٧ × ٧ = ٤٩ $\mathrm{\pi }$

(✔)

هـ) المساحة الجانبية لمكعب طول حرفه س سم = ٦ س^٢ سم^٢ (×)

المساحة الجانبية للمكعب = مساحة الوجه × ٤

= س × س × ٤

= ٤ س^٢

(×)

(٢) أكمل:

أ) إذا كانت س (-٣، ٢)، ص (-٣، -٢) فإن طول $\overline{س ص}$ = ......

$\left|\mathrm{٢} - (-\mathrm{٤})\right| = \left|\mathrm{٢} + \mathrm{٤}\right| =\left|\mathrm{٦}\right|$ = ٦ وحدة طول

ب) صورة النقطة أ (٠، ٤) بالانتقال (س - ٢، ص + ١) هي النقطة أ (.....، .....)

(٠ - ٢، ٤ + ١) = (-٢، ٥)

جـ) مساحة الدائرة = ......، محيط الدائرة = ......

مساحة الدائرة = $\mathrm{\pi }$ نق^٢، محيط الدائرة = ٢ $\mathrm{\pi }$ نق

د) إذا كانت مساحة أحد أوجه مكعب ٢٥ سم^٢ فإن مساحته الجانبية = ...... سم^٢، ومساحته الكلية = ...... سم^٢

المساحة الجانبية للمكعب = مساحة الوجه × ٤

= ٢٥ × ٤ = ١٠٠ سم^٢

المساحة الكلية للمكعب = مساحة الوجه × ٦

= مساحة الوجه × ٦

= ٢٥ × ٦ = ١٥٠ سم^٢

هـ) مساحة دائرة طول قطرها ٢٠ سم = ..... سم^٢

نق = ١٠ سم

مساحة الدائرة = $\mathrm{\pi }$ نق^٢

= $\mathrm{\pi }$ × ١٠ × ١٠

= ٣,١٤ × ١٠ × ١٠

= ٣١٤ سم^٢

(٣) ارسم مستوى الإحداثيات ثم حدد فيه النقاط التالية:

أ (٢، ٢)، ب (١، ٠)، جـ (٣، ٠)، د (٤، ٢) أجب عما يأتي:

• ما اسم الشكل أ ب جـ د ولماذا؟

متوازي أضلاع لأن كل ضلعان متقابلات متوازيان ومتساويان.

• ارسم أَ بَ جـَ د! بانتقال مقداره ٤ وحدات في الاتجاه الموجب لمحور الصادات $\underset{و ص}{\leftarrow }$

أَ (٢، ٦)، بَ (١، ٤)، جـَ (٣، ٤)، ء (٤، ٦)

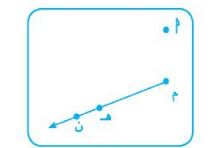
(٤) من الشكل المقابل: أوجد صورة النقطة أ بانتقال م هـ في اتجاه $\underset{م ن}{\leftarrow }$

(٥) على المستوى الإحداثي المقابل:

أ) حدد النقاط التالية: أ (٢، -٢)، ب (١، ١)، جـ (١، ٦)

ب) أوجد أَ صورة أ بانتقال (٢، -١)

(٢ +٢، -٢-١) = أَ (٤، -٣)

جـ) أوجد $\overline{بَ \mathrm{جـ}َ}$ صورة $\overline{ب \mathrm{جـ}}$ بانتقال (٣، ١)

ب َ = (٤، ٢)

جـَ = (٤، ٧)

د) أوجد ب جـ، ب بَ

ب جـ = ٥ وحدة طول

ب بَ =

هـ) احسب محيط ومساحة الشكل ب بَ جـَ جـ

مساحة متوازي الأضلاع = طول القاعدة × الارتفاع

= ٥ × ٣

= ١٥ وحدة مربعة.

و) ادرس تماثل الشكل ب بَ جـَ جـ

غير متماثل.

(٦) أكمل الجدول التالي:

(٧) دائرة محيطها ٦٦ سم، احسب مساحة سطحها. ($\mathrm{\pi }$ ≈ $\frac{\mathrm{٢٢}}{\mathrm{٧}}$)

نصف القطر = المحيط ÷ ٢$\mathrm{\pi }$

= ٦٦ ÷ (٢ × $\frac{\mathrm{٢٢}}{\mathrm{٧}}$) = ١٠,٥ سم.

المساحة = $\frac{\mathrm{٢٢}}{\mathrm{٧}}$ × ١٠,٥ × ١٠,٥ = ٣٤٦,٥ سم^٢

(٨) في الشكل المقابل دائرة م، طول نصف قطرها ٧,٧ سم قسمت إلى ثلاثة قطاعات دائرية متساوية، أوجد مساحة سطح القطاع الواحد (مقرباً الناتج لأقرب عدد صحيح (اعتبر$\mathrm{\pi }$ ≈ $\frac{\mathrm{٢٢}}{\mathrm{٧}}$)

مساحة الدائرة = $\mathrm{\pi }$ نق^٢

= $\frac{\mathrm{٢٢}}{\mathrm{٧}}$ × ٧,٧ × ٧,٧

= ١٨٦,٣٤ سم^٢

مساحة القطاع الواحد = ١٨٦,٣٤ ÷ ٣ = ٦٢ سم^٢

(٩) تورتة عيد م يلاد دائرية الشكل قطرها ٢٥ سم، قسمت إلى ٨ أجزاء متساوية، احسب مساحة سطح الجزء الواحد، (مقرباً الناتج لأقرب عدد صحيح) ($\mathrm{\pi }$ ≈ $\frac{\mathrm{٢٢}}{\mathrm{٧}}$)

مساحة التورتة = $\mathrm{\pi }$ نق^٢ = ٣,١٤ × ١٢,٥ × ١٢,٥ = ٤٩٠,٦٢٥ سم^٢

مساحة الجزء الواحد = مساحة التورتة ÷ ٨

= ٤٩٠,٦٢٥ ÷ ٨

= ٦١ سم^٢

(١٠) مكعب محيط قاعدته ٢٨ سم، احسب مساحته الجانبية ومساحته الكلية.

طول الحرف = $\frac{\mathrm{٢٨}}{\mathrm{٤}}$ = ٧ سم.

المساحة الجانبية = ٧ × ١٧ × ٤ = ١٩٦ سم^٢

المساحة الكلية = ٧ × ٧ × ٦ = ٢٩٤ سم^٢

(١١) خزان للمياه على شكل مكعب طول حرفه من الداخل ١,٥ متراً، يراد طلائه بمادة تمنع الصدأ المربع ١٥ جنيهاً - احسب تكلفة دهان الخزان.

المساحة الكلية للمكعب = مساحة الوجه × ٦

= ١,٥ × ١,٥ × ٦

= ١٣,٥ م^٢

تكلفة دهان الخزان = المساحة الكلية × ١٥

= ١٣,٥ × ١٥

= ٢٠٢,٥ جنيه.

(١٢) عند طي الشكل المقابل فإن:

• المجسم الناتج هو: ........

متوازي مستطيلات.

• المساحة الجانبية للمجسم الناتج = .....

المساحة الجانبية = محيط القاعدة × الارتفاع

= ٦ × ٤ × ١٥

= ٣٦٠ سم^٢

• المساحة الكلية للمجسم الناتج = ......

المساحة الكلية = المساحة الجانبية + مساحتي القاعدة

= ٣٦٠ + ٧٢

= ٤٣٢ سم^٢

(١٣) حجرة أرضيتها مربعة الشكل، طول ضلعها ٤ أمتار وارتفاعها ٣ أمتار، لها باب عرضه ٩٠ سم طوله ٢ متراً، لها شباكان متساويان في المساحة كل منهما مستطيل طوله ١٦٠ سم وعرضه ١٠٠ سم. احسب تكلفة طلاء جدران الغرفة بدهان تكلفة المتر المربع منه ٩ جنيهات.

المساحة الجانبية = ٤ × ٤ × ٣ = ٤٨ م^٢

مساحة الباب = ٠,٩ × ٢ = ١,٨ م^٢

مساحة الشبكان = ١,٦ × ١ × ٢ = ٣,٢ م^٢

مجموع مساحة الباب والنسبتان = ٣,٢ + ١,٨ = ٥ م^٢

صافي المساحة = ٤٨ - ٥ = ٤٣ م^٢

التكلفة = ٤٣ × ٩ = ٣٨٧ جنيه.