الدرس الأول تشابه المضلعات
١) بين أياً من أزواج المضلعات التالية تكون متشابهة، واكتب المضلعات المتشابهة بترتيب الرؤوس المتناظرة، وحدد معامل التشابه (الأطوال مقدرة بالسنتيمترات).
أ) .JPG)
الشكل س ص ع ل مستطيل، س ص = ٣٠ سم.
= ، =
إذاً المضلعان أ ب جـ ء، س ص ع ل غير متشابهان.
ب) .JPG)
الشكل أ ب جـ ء معين.
ق ( أ) = ق ( جـ) = = ١١٠°
الشكل س ص ع ل معين
ق ( س) = ق ( ع) = = ٧٠°
ر ( أ) = ق ( ص)، ق ( ب) = ق ( س)، ق ( جـ) = ق ( ل)
ق ( ء) = ق ( ع) (١)
،
(٢)
من (١) و (٢) نجد أن المضلعان متشابهان. نسبة التشابه =
جـ) 
ق ( ب) = ق ( ء)
ق ( جـ) = ق ( و)
ق ( أ) = ق ( هـ) (١)
=
(٢)
من (١) و (٢) نجد أن ب أ جـ يشابه المثلث ء و هـ.
د) .JPG)
بما أن //
إذاً ق ( أ) = ١٨٠° - ق ( ب)
بما أن
إذاً ق ( ع) = ١٨٠° - ق ( ل)
بما أن ق ( ب) = ق ( ل)
إذاً ق ( أ) = ق ( ع)
ق ( ب) = ق ( ل) = ق ( جـ) = ق ( س) = ق ( أ) = ق ( ع)
إذاً ق ( ء) = ق ( ص) (١)
= ، ، ، (٢)
من ١) و٢) المضلع أ ب جـ ء يشابه المضلع ع ل س ص
٢) إذا كان المضلع أ ب جـ ء المضلع س ص ع ل، أكمل:
أ)
إذاً
ب) أ ب × ع ل = س ص × ......
من الطرفين بالوسطين نجد
أ ب × ع ل = س ص × جـ ء
جـ)
د)
٣) المضلع أ ب جـ ء المضلع س ص ع ل. فإذا كان: أ ب = ٣٢ سم، ب جـ = ٤٠ سم، س ص = ٣م - ١، ص ع = ٣م + ١. أوجد قيمة م العددية.
بما أن المضلع أ ب جـ ء يشابه المضلع س ص ع ل
إذاً
٤ (٣م + ١) = ٥ (٣م - ١)
١٢م + ٤ = ١٥م - ٥
-١٥م + ١٢م = -٥ -٤
-٣م = -٩ نقسم على -٣
م = ٣
٤) مستطيل بعداه ١٠سم، ٦سم. أوجد محيط ومساحة المستطيل آخر مشابه له إذا كان:
أ) معامل التشابه ٣
نفرض أن المستطيل المطلوب أَ بَ جـَ ءَ المستطيل المعطى أ ب جـ ء
بما أن المستطيل أَ بَ جـَ ءَ يشابه المستطيل أ ب جـ ء
إذاً = ٣
= ٣
= ٣ أ َ بَ = ١٠ × ٣ = ٣٠ سم.
= ٣ بَ جـَ = ٦ × ٣ = ١٨
= ٣
محيط المستطيل أَ بَ جـَ ءَ = ٣٢ × ٣ = ٩٦ سم.
مساحة المستطيل أَ بَ جـَ ءَ = أَ بَ × جـَ ءَ = ٣٠ × ١٨ = ٥٤٠ سم٢
ب) معامل التشابه ٠,٤
= ٠,٤
إذاً = ٠,٤ أَ بَ = ٤سم.
= ٠,٤ بَ جـَ = ٢,٤
= ٠,٤
محيط المستطيل أَ بَ جـَ ءَ = ٣٢ × ٠,٤ = ١٢,٨ سم.
مساحة المستطيل أَ بَ جـَ ءَ = أَ بَ × جـَ ءَ = ٤ × ٢,٤ = ٩,٦ سم٢
٥) في كل من الأشكال التالية المضلع م١ المضلع م٢ المضلع م٣ أوجد معامل تشابه كل من المضلع م١ المضلع م٢ المضلع م٣.
أ) .JPG)
نفرض أن طول ضلع المعين = ل وحدة
إذاً طول قطر المربع = ل وحدة طول.
أ ب = ل، جـ ء = ٣ ل، هـ و = ٤ ل
معامل تشابه المضلع م١ للمضلع م٣
= = = ٤
معامل تشابه المضلع م٢ للمضلع م٣
= = = ٣
ب) .JPG)
أ ب = ٨ وحدة طول، جـ ء = ١٢ وحدة طول.
هـ ء = ٨ وحدة طول
معامل تشابه المضلع م١ للمضلع م٣
= ١ المضلعان منطبقان.
معامل تشابه المضلع م٢ للمضلع م٣
=
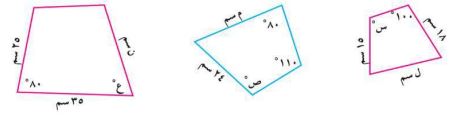
٦) المضلعات الثلاثة التالية متشابهة. أوجد القيمة العددية للرمز المستخدم في القياس.
ص = ١٠٠، ع = ٣٦٠ - (١٠٠ + ١١٠ + ٨٠) = ٧٠°
الشكل الأول والثاني
=
الشكل الثاني والثالث
الشكل الأول والثاني
=
= ل = ٢١، = = ن = ٣٠
م = ٢٨
٧) مستطيلان متشابهان بعدا الأول ٨سم، ١٢سم، ومحيط الثاني ٢٠٠سم. أوجد طول المستطيل الثاني ومساحته.
محيط المستطيل الأول = ٢ (٨ + ١٢) = ٤٠
نفرض أن طول المستطيل المطلوب = س
عرض المستطيل = ص
س = = ٦٠ سم.
ص = = ٤٠ سم.
مساحة المستطيل = ٦٠ × ٤٠ = ٢٤٠٠سم٢

.JPG)
.JPG)