الدرس الرابع: تطبيقات التشابه في الدائرة
١) باستخدام الآلة الحاسبة أو الحساب العقلي، أوجد قيمة س العددية في كل من الأشكال التالية. (الأطوال مقدرة بالسنتمترات)
أ) .JPG)
٤ × س = ٣ × ٨
س = = ٦
ب) .JPG)
٦ × ١٨ = ٣س × ٤س
١٢ س٢ = ٦ × ٨
س٢ = = ٩
س = ٣
جـ) .JPG)
(٢س - ٦) × ٦ = ٧ × ١٢
٢س - ٦ = ١٤
٢س = ١٤ + ٦
س = ١٠
د) .JPG)
٦ × (٦ + س) = ٥ × ١٢
٦ + س = ١٠
س = ٤
هـ) .JPG)
س (س + ١٠) = ٩ × ١٦
س٢ + ١٠س - ١٤٤ = صفر
(س - ٨) (س + ١٨) = ٠
س = ٨ سم.
و) .JPG)
س (٤س) = ٨ (س + ١٢)
س٢ = ٢س + ٢٤
س٢ -٢س - ٢٤ = صفر
(س - ٦) (س + ٤) = ٠
س = ٦
ز) .JPG)
س٢ = ٧ × ١٦
س = ٤
ح) .JPG)
٥ (س + ٥) = ٤٩
س + ٥ = = ٩,٨
س = ٩و٨ - ٥ = ٤,٨ سم.
ط) .JPG)
س (٢س) = ٦٤
٢س٢ = ٦٤
س٢ = ٣٢
س = ٤
ي) .JPG)
س٢ = جـ ب × جـ أ
س٢ = ٧ × ١٦
س = ٤
ك) .JPG)
ء ك × ٨ = ١٠ × ٣,٢
ء ك = ٤سم.
س٢ = ٤ × ١٦
س = ٨
ل) .JPG)
م جـ = جـ أ
جـ أ = ٩
س × ٩ = ٣ × ١٥
س = = ٥
٢) في أي من الأشكال التالية تقع النقط أ، ب، جـ، ء على دائرة واحدة؟ فسر إجابتك. (الأطوال مقدرة بالسنتمترات)
أ) .JPG)
هـ أ × هـ ب = ٦ × ٧ = ٤٢
هـ أ × هـ ء = ٥ × ٨,٤ = ٤٢
إذاً أ، ب، جـ، ء تقع على استقامة واحدة.
ب) .JPG)
أ، ء، ب تقع على استقامة واحدة إذاً أ، ب، جـ، ء لا تقع على استقامة واحدة.
جـ) .JPG)
ب، ء، أ تقع على استقامة واحدة إذاً أ، ب، جـ، ء لا تقع على استقامة واحدة.
٣) في أي من الأشكال مماس للدائرة المارة بالنقط ب، جـ، ء.
أ) .JPG)
(أ ب)٢ = ١٦
أ ء × أ جـ = ٢ × ٨ = ١٦
إذاً (أ ب)٢ = أ ء × أ جـ
أ ب مماس للدائرة المارة بالنقط ب، جـ ء
ب) .JPG)
(أ ب)٢ = ٣٦
أ ء × أ جـ = ٥ × ٩ = ٤٥
إذاً (أ ب)٢ أ ء × أ جـ
أ ب ليس مماس للدائرة.
جـ) .JPG)
(أ ب)٢ = (ب جـ)٢ - (جـ أ)٢
= ٢٩ - ٢٥
= ٤
أ ء × أ جـ = ١ × ٥ = ٥
٤) دائرتان متقاطعتان في أ، ب، جـ، ، جـ رسم من جـ القطعتان ، مماستان للدائرتين عند س، ص. أثبت أن جـ س= جـ ص.
بما أن (جـ س)٢ = جـ ب × جـ أ
(جـ ص)٢ = جـ ب × جـ أ
إذاً (جـ س)٢ = (جـ ص)٢
جـ س = جـ ص
٥) في الشكل المقابل: الدائرتان م، ن متماستان عند هـ يمس الدائرة م عند ب ويمس الدائرة ن عند جـ، يقطع الدائرتين عند و، ء على الترتيب حيث أ و = ٤سم، و هـ = ٥سم، هـ ء = ٧ سم. أثبت أن ب منتصف
في الدائرة م
أ و × أ هـ = (أ ب)٢
(أ ب)٢ = ٤ × ٩ أ ب = ٦ سم.
في الدائرة ن
أ هـ × أ ء = (أ جـ)٢
(أ جـ)٢ = ٩ × ١٦ أ جـ = ٦ سم.
إذاً أ ب = أ جـ
إذاً ب في منتصف أ جـ
٦) في الشكل المقابل: ل حيث س ل = ٤سم، ص ل = ٨سم، م حيث س م = ٦سم، ع م = ٢سم أثبت أن:
أ) س ل م س ع ص
س ل = ٤سم، س م = ٦
س ع = ٨ سم، س ص = ١٢
الزاوية س زاوية مشتركة.
إذاً س ل م س ع ص
ب) الشكل ل ص ع م رباعي دائري.
ق ( س ل م) = ق ( س ع ص)
إذاً الزاوية الخارجة تساوي المقابلة للمجاورة لها.
إذاً الرباعي دائري.
٧) = {هـ}، أ هـ = ب هـ، ء هـ = هـ جـ، إذا كان ب هـ = ٦سم، جـ هـ = ٥سم. أثبت أن النقط أ، ب، جـ، ء تقع على دائرة واحدة.
أ هـ = ب هـ = = ٢,٥ سم
ء هـ = = × ٥ = ٣ سم.
هـ أ × هـ ب = ٢,٥ × ٦ = ١٥ سم.
هـ ء × هـ جـ = ٣ × ٥ = ١٥
إذاً هـ أ × هـ ب = هـ ء × هـ جـ
إذاً أ، ب، جـ، ء تقع على دائرة واحدة.
٨) أ ب جـ مثلث، ء حيث ء ب = ٥سم، ء جـ = ٤سم. إذا كان أ جـ = ٦سم. أثبت أن:
أ) مماسة للدائرة التي تمر بالنقط أ، ب، ء.
(أ جـ)٢ = ٣٦
جـ ء × جـ ب = ٤ × ٩ = ٣٦
إذاً أ جـ مماس للدائرة التي تمر بالنقط أ، ب، ء
ب) أ جـ ء ب جـ أ
جـ مشتركة أ جـ ء ب جـ أ
جـ) مـ ( أ ب ء) : مـ ( أ ب جـ) = ٥ : ٩
مـ ( أ جـ ء) : مـ ( ب جـ أ) : مـ ( أ جـ ء)
٤ : ٩ : ٩ - ٤ = ٥
مـ ( أ جـ ء) : مـ ( أ ب جـ) = ٥ : ٩
٩) دائرتان متحدتا المركز م، طولا نصفي قطريهما ١٢سم، ٧سم، رسم الوتر في الدائرة الكبرى ليقطع الدائرة الصغرى في ب، جـ على الترتيب. أثبت أن: أ ب × ب ء = ٩٥
نرسم القطر س ص
أ ب × ب ء = س ب × ب ص
أ ب × ب ء = ٥ × ١٩ = ٩٥ وهو المطلوب.
١٠) أ ب جـ ء مستطيل فيه أ ب = ٦سم، ب جـ = ٨سم. رسم فقطع في هـ، في و.
أ) أثبت أن (أ ب)٢ = أو × أ ء.
بما أن
فإن ق ( جـ هـ و) + ق ( ء) = ١٨٠°
إذاً الشكل جـ هـ و ء رباعي دائري أ و × أ ء = أ هـ × أ جـ (١)
في المثلث أ ب جـ (أ ب)٢ = أ هـ × أ جـ حسب إقليدس (٢)
من ١) و٢) (أ ب)٢ = أو × أ ء.
ب) أوجد طول .
(أ ب)٢ = أو × أ ء.
(٦)٢ = أ و × ٨ أ و = = ٤,٥ سم
١١) الربط مع الصناعة: كسر أحد تروس آلة ولاستبداله مطلوب معرفة طول نصف قطر دائرته. يبين الشكل المقابل جزءاً من هذا الترس، والمطلوب تعيين طول نصف قطر دائرته.
العمل نكمل رسم الدائرة نرسم القطر عمودي من منتصف الوتر.
× ٤ = × (٢ نق - ٢)
نق - ١ = ٤
نق = ٥سم.
١٢) الربط مع البيئة: يبين الشكل المقابل مخططاً لحديقة على شكل دائرة بها طريقان يتقاطعان عند نافورة المياه. أوجد بعد نافورة المياه عند المدخل جـ.
١٥ × س = ١٠ × ١٢
س = = ٨م.
١٣) الربط مع المنزل: تستخدم هدى شبكة لشي اللحوم على شكل دائرة من السلك، طول قطرها ٥٠ سم، يدعمها من الوسط سلكان متوازيان ومتساويان في الطول كما في الشكل المقابل، والبعد بينهما ١٠ سم. احسب طول كل من سلكي الدعامة.
السلكان متوازيان ومتساويان في الطول.
بما أن السلكان على بعد متساوي من المركز.
يرسم قطر الدائرة عمودي على السلك
بما أن المركز يبعد عن السلك ٥سم. نصف المسافة بين السلكين.
س × س = ٢٠ × ٣٠ = ٦٠٠
س = ١٠ سم.
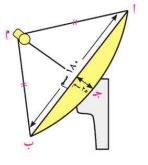
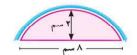
١٤) الربط مع الاتصال: تنقل الأقمار الصناعية البرامج التليفزيونية إلى كافة مناطق الأرض، وتستخدم أطباق خاصة لاستقبال إشارات البث التليفزيوني، وهي أطباق مقعرة على شكل جزء من سطح كرة. يبين الشكل المقابل مقطعاً في أحد هذه الأطباق، طول قطره ١٨٠ سم، والمطلوب حساب طول نصف قطر كرة تقعره .
٢٥ × (٢نق - ٢٥) = ٩٠ × ٩٠
٢نق - ٢٥ =
٢نق - ٢٥ = ٣٢٤
٢نق = ٣٤٩
نق = ١٧٤,٥ سم.

.JPG)
.JPG)
.JPG)
.JPG)
.JPG)

.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)