الدرس الثالث: نظريات المثلث المتساوي الساقين
١) .JPG)
أ جـ = ٣ سم.
س ع = ٣ سم
ء هـ = ١٠ سم، ق ( هـ) = ٦٠°
هـ و = ١٠ سم، ق ( م ء و) = ٦٠°
٢) في الشكل المقابل: أ ب = أ جـ، ق ( ب أ جـ) = ٤٨°
ينصف ب جـ أ ويقطع في ء
.JPG) ق (ب)، ق ( ب جـ ء)
ق (ب)، ق ( ب جـ ء)
أ ب = أ جـ
- ق (ب) = ق ( جـ) = = ٦٦°
منصف للزاوية ( جـ)
ق (ب جـ ء) = = ٣٣°
٣) في الشكل المقابل: أ ب جـ مثلث فيه أ جـ = ب جـ، // ، ق ( ء أ جـ) = ٣٠°
.JPG) قياسات زوايا أ ب جـ
قياسات زوايا أ ب جـ
//
ق ( ء أ جـ) ق ( جـ) = ٣٠° بالتبادل.
أ جـ = ب جـ
ق ( جـ أ ب) = ق ( جـ ب أ)
= = ٧٥°
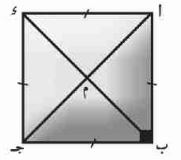
٤) في الشكل المقابل ع ، س ع = ص ع
ق ( ل ع س) = ١٣٠°، //
.JPG) ق (م ل ص)
ق (م ل ص)
- في ع س ص
ع س = ع ص
ق ( س) = ق ( ص) (١)
( ل ع ص) خارجه عن المثلث ع س ص
ق ( ل ع ص) = ق س + ق ص
نعوض في (١)
١٣٠ = ق س + ق س
١٣٠ = ٢ ق س
ق س = = ٦٥°
ق ص = ٦٥°
- //
ق ص = ق ل بالتبادل = ٦٥°
٥) في الشكل المقابل أ ب = أ جـ، ق ( ب) = (٢س + ١٣)° ق ( جـ) = (٣س - ١٧)°
.JPG) قياسات زوايا أ ب جـ
قياسات زوايا أ ب جـ
أ ب = أ جـ
ق ( ب) = ق ( جـ)
٢س + ١٣ = ٣س - ١٧
١٣ + ١٧ = ٣س - ٢س
س = ٣٠
ق ( ب) = ٢س + ١٣
= ٢ × ٣٠ + ١٣
= ٧٣°
ق ( جـ) = ٧٣°
ق ( أ) = ١٨٠ - ١٤٦
= ٣٤°
٦) في الشكل المقابل أ ب جـ مثلث متساوي الساقين فيه أ ب = أ جـ، ء بحيث ب ء = هـ جـ
أولاً: أ ء هـ متساوي الساقين
أ ب = أ جـ
ق ( ب) = ق ( جـ)
أ ب ء، أ جـ هـ
فيهما
- أ ب = أ جـ
- ب ء = هـ جـ
- ق ( ب) = ق ( جـ)
أ ب ء، أ جـ هـ
ينتج أن أ ء = أ هـ
ق ( أ ء هـ) = ق ( أ هـ ء)
أ ء هـ متساوي الساقين
ثانياً: أ ء هـ أ هـ ء
بما أن المثلث متساوي الساقين
فإن أ ء هـ أ هـ ء
٧) في الشكل المقابل: أ ب جـ مثلث متساوي الأضلاع. و ، د ، ق ( ء و جـ) = ٣٠°
 ء جـ و متساوي الساقين.
ء جـ و متساوي الساقين.
أ ب جـ متساوي الأضلاع
قياس كل زاوية من زواياه = ٦٠°
ق ( أ جـ ب) = ٦٠°
ق ( أ جـ و) = ١٨٠° لأنها مستقيمة.
ق ( ء جـ و) = ١٨٠ - ٦٠ = ١٢٠°
في ء جـ و
ق ( ء) = ١٨٠ - ١٥٠ = ٣٠°
( ء) = ق ( و) = ٣٠°
٨) في الشكل المقابل ينصف أ ب جـ، ويقطع في ء، // .
 هـ ب ء متساوي الساقين.
هـ ب ء متساوي الساقين.
ينصف ( ب)
ق ( ١) = ق ( ٢) (١)
//
ق ( هـ ء ب) = ق ( ٢) بالتبادل
ق ( هـ ء ب) = ق ( ١)
هـ ب ء متساوي الساقين.
٩) أ ب جـ مثلث فيه ء ، هـ بحيث كان ب ء = ب هـ، فإذا كان //
 أ ب = ب جـ
أ ب = ب جـ
في ب ء هـ
ب ء = ب هـ
ق ( ١) = ق ( ٢) (١)
//
ق ( ١) = ق ( ٣) بالتناظر
ق ( ٢) = ق ( ٤) بالتناظر
ولكن من ١
ق ( ٣) = ق ( ٤)
إذاً أ ب = ب جـ
١٠) أ ب جـ مثلث فيه أ ب = أ جـ، ينصف أ ب جـ، ينصف أ جـ ب
 ء ب جـ متساوي الساقين.
ء ب جـ متساوي الساقين.
أ ب = أ جـ
ق ( ب) = ق ( جـ) (١)
ينصف (ب)
ق ( ء ب جـ) = ق ( ب)
ينصف ( جـ)
ق ( ء جـ ب) = ق ( جـ)
من ١ نستنتج أن
ق ( ء ب جـ) = ق ( ء جـ ب)
ء ب = ء جـ
المثلث متساوي الساقين

.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)