تمارين عامة على متوسطات المثلث والمثلث المتساوي الساقين
١) في الشكل المقابل
أ ب = أ جـ، ب جـ = ١٠ سم، ق ( ب أ ء) = ٣٠°،
أولاً: أوجد طول كل من ، .
- أ ب = أ جـ،
ب ء = جـ ء ب ء = ب جـ = ٥ سم.
- أ ب جـ فيه ق ( أ ء ب) = ٩٠°
ق ( ب أ ء) = ٣٠°
أ ء = ٢ ب ء = ١٠ سم.
أ ء =
ثانياً: ما عدد محاور تماثل المثلث أ ب جـ؟
أ ب ء فيه ق ( أ ء ب) = ٩٠°
ق ( ب أ ء) = ٣٠°
ق ( ب) = ١٨٠ - (٩٠ + ٣٠) = ٦٠°
أ ب جـ فيه أ ب = أ جـ، ق ( ب) = ٦٠°
أ ب جـ متساوي الأضلاع
عدد محاور التماثل أ ب جـ = ٣ محاور
ثالثاً: ما مساحة أ ب جـ؟
مساحة أ ب جـ ء = ب جـ × أ ء
= × ١٠ × ٥
= ٥ × ٥ = ٢٥
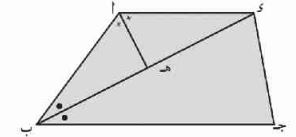
٢) في الشكل المقابل
أ ب = أ جـ، ء ، هـ
ينصف ء ب جـ،
ينصف ب جـ هـ
أولاً: ب و جـ متساوي الساقين
أ ب = أ جـ
ق ( أ ب جـ) = ق ( أ جـ ب) = ق ( ب جـ هـ)
ق ( جـ ب ء) = ق ( ب جـ هـ)
ق ( و ب جـ) = ق ( و جـ ب)
و ب = و جـ
ب و جـ متساوي الساقين.
ثانياً: محور تماثل
أ ب = أ و (١)
و ب = و جـ (٢)
من ١) و ٢) محور تماثل
٣) في الشكل المقابل
أ ب = جـ ب، أ ء = جـ ء
ينصف أ ء جـ
أ ء = جـ ء (١)
أ ب = جـ ب (٢)
محور تماثل
في أ ء جـ
ء أ = ء جـ،
ينصف أ ء جـ
ينصف أ ء جـ
ينصف أ ب جـ
محور تماثل
و أ = و جـ
في أ و جـ
ينصف أ و جـ
ينصف أ ب جـ
٤) في الشكل المقابل
// ، أ ء // أ هـ
برهن أن: أ ب = أ جـ.
أ ء هـ فيه أ ء = أ هـ
ق ( أ ء هـ) = ق ( أ هـ ء)
//
ق ( ب) = ق ( أ ء هـ) بالتناظر
ق ( جـ) = ق ( أ هـ ء) بالتناظر
ق ( ب) = ق ( جـ)
في المثلث أ ب جـ
أ ب = أ جـ
٥) في الشكل المقابل:
أ ب = أ جـ = أ ء = جـ ء
ق ( ب أ جـ) = ٤٠°
أوجد ق ( ب جـ ء)
في أ ب جـ
أ ب = أ جـ
ق ( ب) = ق ( أ جـ ب)
= = ٧٠°
في أ جـ ء
أ جـ = جـ ء = أ ء
ق ( أ جـ ء) = ٦٠ °
ق ( ب جـ ء) = ٧٠ + ٦٠ = ١٣٠°
٦) في الشكل المقابل:
أ ب جـ مثلث فيه ق ( ب) = ق ( جـ)
أوجد محيط المثلث
ق ( ب) = ق ( جـ)
أ ب = أ جـ
٢س -١ = س + ٣
٢س - س = ٣ + ١
س = ٤
أ ب = ٢س -١ = ٢ × ٤ - ١ = ٨ - ١ = ٧ وحدة طول.
أ جـ = س + ٣ = ٤ + ٣ = ٧ وحدة طول.
ب جـ = ٩ - س = ٩ - ٤ = ٥ وحدة طول.
محيط المثلث = ٧ + ٧ + ٥ = ١٩
٧) في الشكل المقابل:
أ ب جـ ء شكل رباعي فيه // ،
ينصف أ ب جـ
ينصف ب أ ء
أثبت أن:
أولاً: أ ب = أ ء
// ، قاطع لهما.
ق ( أ ء ب) = ق ( ء ب جـ) بالتبادل.
ينصف أ ب جـ
ق ( ء ب جـ) = ق ( أ ب ء)
ق ( أ ء ب) = ق ( أ ب ء)
في المثلث أ ء = أ ب
ثانياً:
ينصف ب أ ء
ب هـ = ء هـ
ثالثاً: ب هـ = هـ ء
ينصف ب أ ء
ب هـ = ء هـ
١) باستخدام المسطرة والفرجار ارسم أ ب جـ الحادة وفي الجهة الأخرى من ارسم //
٢) في الشكل المقابل أ ب جـ ء مستطيل، قطر فيه، ينصف ب أ جـ،
حيث = {هـ}
= {م}
 ء أ = ء هـ.
ء أ = ء هـ.
في أ ب جـ ، أ م هـ
ق (ب أ و) = ق ( م أ هـ)
ق (أ ب و) = ق ( أ م هـ) = ٩٠°
ق (أ و ب) = ق ( هـ) (١)
، قاطع لهما.
ق (هـ و ب) = ق ( ء أ هـ) بالتبادل (٢)
من (١) و (٢)
ق (ء أ هـ) = ق ( هـ)
ء أ = ء هـ

.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)

.JPG)