الدرس الثالث: الزاوية المحيطية المرسومة على نفس القوس
أولاً:
١) في الشكل المقابل: م، ن دائرتان متقاطعتان في أ، ب يقطع الدائرة م في جـ ويقطع الدائرة ن في ء، يقطع الدائرة م في هـ، ويقطع الدائرة ن في و. أثبت أن: ق ( هـ ب جـ) = ق (و ب ء)
= {أ}
ق ( جـ أ هـ) = ق ( و أ ء) بالتقابل بالرأس. (١)
جـ أ هـ ، جـ ب هـ مشتركتان في
ق ( جـ أ هـ) = ق ( جـ ب هـ) (٢)
و أ ء، و ب ء مشتركتان في
ق ( و أ ء) = ق ( و ب ء) (٣)
من ١) و ٢) و ٣)
ق ( جـ ب هـ) = ق ( و ن ء)
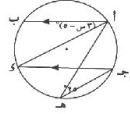
٢) في الشكل المقابل: ، وتران متساويان في الطول في الدائرة، = {هـ}. أثبت أن: أ جـ هـ متساوي الساقين.
أ ب = جـ ء بحذف ق () من الطرفين.
ق () = ق ()
ق ( ب أ جـ) = ق ( أ جـ ء)
في أ جـ هـ
ق ( هـ أ جـ) = ق ( هـ جـ أ)
أ جـ هـ متساوي الساقين.
أ ب = جـ ء
٣) في الشكل المقابل: أ ب = أ جـ، هـ أثبت أن: ق ( أ هـ ب) = ق ( أ هـ جـ)
البرهان: أ ب = أ جـ
ق () = ق ()
ق ( أ هـ ب) = ق ( أ هـ جـ)
القوسان المتساويان في القياس يحصران زاويتان محيطيتان متساويتان في القياس.
٤) بين في أي من الأشكال الآتية يمكن رسم دائرة تمر بالنقط أ، ب، جـ، ء؟ اذكر السبب.
أ) .JPG)
النقط أ، ب، جـ، ء تمر فيهما دائرة واحدة.
لأن ق ( أ ء ب) = ق ( أ جـ ب)
زاويتان متساويتان في القياس وتشتركان في القاعدة من نفس الجهة
ب) .JPG)
النقط أ، ب، جـ، ء تمر فيهما دائرة واحدة.
لأن ق ( أ ب ء) = ق ( أ جـ ء)
زاويتان متساويتان في القياس وتشتركان في القاعدة من نفس الجهة
جـ) .JPG)
النقط أ، ب، جـ، ء تمر فيهما دائرة واحدة.
لأن ق ( أ جـ ب) = ق ( أ ء ب)
زاويتان متساويتان في القياس وتشتركان في القاعدة من نفس الجهة
د) .JPG)
النقط أ، ب، جـ، ء تمر فيهما دائرة واحدة.
لأن ق ( أ ء ب) = ق ( أ جـ ب)
زاويتان متساويتان في القياس وتشتركان في القاعدة من نفس الجهة
هـ) .JPG)
النقط أ، ب، جـ، ء تمر فيهما دائرة واحدة.
لأن ق ( أ ء ب) = ق ( أ جـ ب)
زاويتان متساويتان في القياس وتشتركان في القاعدة من نفس الجهة
و) .JPG)
النقط أ، ب، جـ، ء لا تمر فيهما دائرة واحدة.
لأن ق ( أ ء ب) ق ( أ جـ ب)

.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)