الدرس الثاني: مساحة متوازي الأضلاع
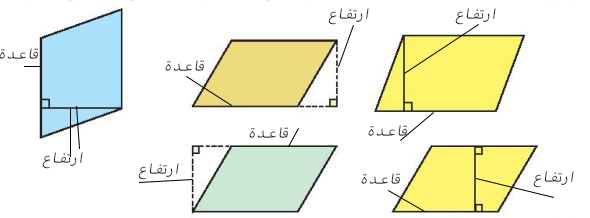
(١) في كل شكل من الأشكال التالية حدد على الرسم قاعدة متوازي الأضلاع، والارتفاع المناظر لها.
(٢) أكمل لإيجاد مساحة كل من الأشكال الملونة:
مساحة متوازي الأضلاع = طول القاعدة × الارتفاع
مساحة الشكل رقم (١) = ..... × ..... = ..... وحدة مربعة.
= ٣ × ٣ = ٩ وحدة مربعة.
مساحة الشكل رقم (٢) = ..... × ..... = ..... وحدة مربعة.
= ٣ × ٤ = ١٢ وحدة مربعة.
مساحة الشكل رقم (٣) = ..... × ..... = ..... وحدة مربعة.
= ٥ × ٣ = ١٥ وحدة مربعة.
مساحة الشكل رقم (٤) = ..... × ..... = ..... وحدة مربعة.
= ٩ + ٩ = ١٨ وحدة مربعة.
(٣) في متوازيات الأضلاع أكمل الجدول:
| طول القاعدة بالسنتمترات | الارتفاع بالسنتمترات | مساحة متوازي الأضلاع بالسنتمترات المربعة |
| ٨ | ٣,٢٥ | ٢٦ |
| ٦,١ | ٩ | ٥٤,٩ |
| ١٥ | ٤,٢ | ٦٣ |
- مساحة متوازي الأضلاع = طول القاعدة × الارتفاع
= ٨ × ٣,٢٥ = ٢٦ سم٢
- الارتفاع = مساحة متوازي الأضلاع ÷ القاعدة
= ٥٤,٩ ÷ ٦,١ = ٩ سم
- طول القاعدة = مساحة متوازي الأضلاع ÷ الارتفاع
= ٦٣ ÷ ٤,٢ = ١٥ سم
(٤) احسب مساحة متوازي الأضلاع في كل من الشكلين التاليين:
أ) .JPG)
مساحة متوازي الأضلاع = طول القاعدة × الارتفاع
= ٦٠ × ٤٠ = ٢٤٠٠ سم٢
ب) .JPG)
مساحة متوازي الأضلاع = طول القاعدة × الارتفاع
= ٥,٨ × ٢٨,٤ = ١٦٤٧,٢سم٢
(٥) في الشكل المقابل أكمل: مساحة متوازي الأضلاع أ ب جـ د = ب جـ × د و = .... سم٢ أيضاً مساحة متوازي الأضلاع = .... × د هـ استنتج طول
مساحة متوازي الأضلاع = طول القاعدة × الارتفاع
= ب جـ × د و
= ٦ × ٣
= ١٨ سم٢.
أيضاً مساحة متوازي الأضلاع = أ ب × د هـ
١٨= ٤,٥ × د هـ
د هـ = ١٨ ÷ ٤,٥ = ٤ سم.
(٦) اختر الإجابة الصحيحة: في الشكل المقابل مساحة متوازي الأضلاع تكون:
أ) ١٣,٦٣ سم
ب) ٧,٦ سم٢
جـ) ١٣,٦٣ سم٢
د) ١٢,٦٣ سم٢
مساحة متوازي الأضلاع = طول القاعدة × الارتفاع
= ٤,٧ × ٢,٩
= ١٣,٦٣
(٧) في الشكل المقابل احسب مساحة متوازي الأضلاع أ ب جـ د، ثم أوجد طول . حيث أ ب = ١٠سم، د هـ = ١٢ سم، د و = ٨ سم.
مساحة متوازي الأضلاع = طول القاعدة × الارتفاع
= ١٠ × ١٢
= ١٢٠ سم٢
وأيضاً مساحة متوازي الأضلاع = طول القاعدة × الارتفاع
طول القاعدة (ب جـ) = ١٢٠ ÷ ٨ = ١٥ سم.
(٨) أكمل: في الشكل المقابل أ ب جـ د متوازي أضلاع. ب جـ = ١٢ سم، فيكون: أ د = ... سم، أ م = .... سم.
أ د = ١٢ سم، أ م = ٦ سم.
مساحة متوازي الأضلاع أ ب جـ د = .... سم٢
مساحة متوازي الأضلاع = طول القاعدة × الارتفاع
= ١٢ × ٧ = ٨٤ سم٢
مساحة المثلث أ ب م = .... سم٢
مساحة المثلث = × ٦ × ٧ = ٢١ سم٢
مساحة الشكل م ب جـ د = .... سم٢
مساحة الشكل م ب جـ د = مساحة متوازي الأضلاع - مساحة المثلث
= ٨٤ - ٢١ = ٦٣ سم٢
(٩) متوازي أضلاع طول قاعدته ٣٤,٧ سم، وارتفاعه ٢٨,١٨ سم. أوجد مساحة سطحه لأقرب جزء من مائة.
مساحة متوازي الأضلاع = طول القاعدة × الارتفاع
= ٣٤,٧ × ٢٨,١٧
= ٩٧٧,٤٩٩ سم٢
≈ ٩٧٧,٥٠ سم٢
(١٠) أيهما أكبر في المساحة: متوازي أضلع طول قاعدته ١٥,٧ سم وارتفاعه ٩,٤ سم؟ أم مثلث طول قاعدته ١٤ سم وارتفاعه ١٨ سم.
مساحة متوازي الأضلاع = طول القاعدة × الارتفاع
= ١٥,٧ × ٩,٤
= ١٤٧,٥٨ سم٢
مساحة المثلث = طول القاعدة × الارتفاع
= × ١٤ × ١٨
= ٧ × ١٨
= ١٢٦ سم٢
مساحة متوازي الأضلاع أكبر
(١١) في الشكل المقابل: // أ ب جـ د متوازي أضلاع، هـ و س ص مستطيل، قارن بين مساحة المستطيل ومساحة متوازي الأضلاع.
مساحة متوازي الأضلاع = طول القاعدة × الارتفاع
= ٦ × ١٠ = ٦٠ سم٢
مساحة المستطيل = الطول × العرض
= ١٠ × ٦ = ٦٠ سم٢
مساحة المستطيل تساوي مساحة متوازي الأضلاع.

.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)