الدرس الأول: مفاهيم هندسية

١) أكمل:

أ) إذا كان ق ( أ) = ٨٠°، ق ( أ) المنعكسة = ....°

٢٨٠°

ب) الزاويتان المتتامتان والمتساويتان في القياس يكون قياس كل منهما = ..... °

٤٥°

جـ) أ، ب متكاملتان، ق(أ) = ٢ ق (ب) = ......°

٦٠°

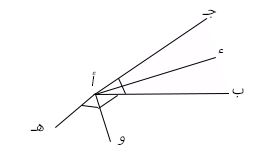
٢) ارسم الزاوية ب أ جـ

[أ] أوجد قياس ب أ جـ

القياس باستخدام المنقلة.

[ب] ارسم أ ء بين الشعاعين . بحيث ق ( ء أ جـ) = ق (ب أ جـ)

[جـ] هل بنصف ب أ جـ

نعم.

[د] مد إلى هـ

[هـ] ارسم منصف ب أ هـ

أوجد قياس الزوايا قبل إجابة (و). (ز)

القياس باستخدام المنقلة.

[و] اذكر أزواج الزوايا المتتامة.

الزاوية ء أ جـ، ب أ و

ب أ ء، هـ أ و.

ء أ حـ، هـ أ و

ب أ ء، ب أ و

[ز] اذكر أزواج الزوايا المتكاملة.

ء أ حـ، ء أ ب

ب أ و، هـ أ و

٣) [أ] ارسم الزوايا التي قياساتها: ٦٠°. ١١٥°. ١٩٥°. ٢٤٥° ثم اكتب نوع كل منها.

[ب] اكتب مكملات الزوايا التي قياساتها: ١٠°. ١١٧°. ٨٢°.

١٠° = ١٧٠°

١١٧° = ٦٣°

٨٢° = ٩٨°

= ٨٧°

[جـ] اكتب متممات الزوايا التي قياساتها: ٣٧°. ٤٨°. ٤٥°.

٣٧° = ٥٣°

٤٨° = ٤٢°

٤٥° = ٤٥°

= ٦٧°

٤) في الشكل المقابل: إذا كانت ب ، ق(ء ب حـ) = ١٣٥°، ينصف ء ب هـ فأوجد كلاً من:

ق ( أ ب ء)، ق (ء ب هـ)، ق (حـ ب هـ)

ق ( أ ب ء) = ١٨٠° - ١٣٥° = ٤٥° لأنها مكملة الزاوية ء ب جـ

ق (ء ب هـ) = ٤٥° لأن أ ب منصف

ق (جـ ب هـ) = ١٣٥° لأنها مكملة الزاوية أ ب هـ

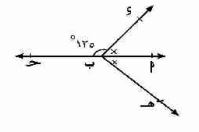
٥) في الشكل المقابل: إذا كان = {م}، منصف ء م هـ

فأوجد قياسات الزوايا التالية: ب م هـ، ء م هـ، أ م حـ ، أ م هـ

لدينا الزاوية حـ م ء = ٩٠° لأنه عمود

ء م هـ = ٩٠°، م ب منصف فإن كلاً من

ء م ب = ب م هـ = ٤٥°

أ م هـ = ١٨٠ - ٤٥ = ١٣٥°

٦) في كل من الأشكال الآتية اذكر قياس الزاوية المشار إليها بالعلامة (؟)

(١)

ق (ب م جـ) = ٣٦٠ - (١٢٠ - ١٠٠)

= ٣٦٠ - ٢٢٠

= ١٤٠°

(٢)

ق (أ م ب) = ٣٦٠ - (١٠٠ + ٧٠ + ٨٠)

= ٣٦٠ - ٢٢٠

= ١٤٠°

(٣)

ق (جـ م ء) = ٣٦٠ - (٩٠ + ٦٠ + ٥٠ + ٤٠)

= ٣٦٠ - ٢٤٠

= ١٢٠°

(٤)

ق (ء م أ) = ٣٦٠ - (١٢٠ + ٨٠ + ٦٠)

= ٣٦٠ - ٢٦٠

= ١٠٠

ق (ء م هـ) = ١٠٠ ÷ ٢ = ٥٠