الدرس الثالث: تطابق المثلثات
١) العلامات المتشابهة تدل على تطابق العناصر المبينة عليها هذه العلامات.
-
هل المثلثان متطابقان؟
-
إذا كان المثلثان متطابقين. اكتب حالة التطابق. إذا كان المثلثان غير متطابقين اذكر السبب.
[أ] .JPG)
متطابقان
الأضلاع الثلاث.
[ب] .JPG)
متطابقان
ضلعين وزاوية محصورة بينهما
[جـ] .JPG)
غير متطابقان.
لا تنطبق الشروط (الضلع ليس مرسوم بينهم).
[د] .JPG)
متطابقان
قائم ضلع ووتر
[هـ] .JPG)
متطابقان
ضلعين وزاوية محصورة بينهما
[و] .JPG)
متطابقان
زاويتين وضلع مرسوم بينهم.
[ز] .JPG)
متطابقان
زاويتين وضلع مرسوم بينهم
[حـ] .JPG)
متطابقان
قائم ضلع ووتر
٢) ادرس الأشكال الآتية وأوجد قيمة س. ص في كل مما يأتي:
[أ] .JPG)
ص = ٤٢°
س = ٤,٨
[ب] .JPG)
س = ١١
ص = ٥٢,٥°
[جـ] .JPG)
س = ١٤
ص = ١٠٣
[د] 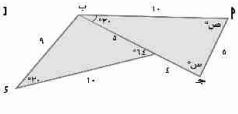
ص = ١٣٦
س = ١٤
[هـ] .JPG)
س = ١٢
ص = ١٧
٣) العلامات المتشابهة تدل على تطابق العناصر المبينة عليها هذه العلامات اذكر المثلثات المتطابقة مع ذكر السبب. ثم اكتب ناتج التطابق.
[أ] .JPG)
و جـ ب، و أ ء
فيهما:
- و جـ = و أ
- و ب = و ء
- ب جـ = أ ء
ينتج أن:
- ق (جـ) = ق ( أ)
- ق (ب) = ق ( ء)
- ق (جـ و ب) = ق ( أ و ء)
[ب] .JPG)
ب أ ء، أ ب جـ
فيهما:
- ق (ء ب أ) = ق ( ب أ جـ)
- ق (ء أ ب) = ق ( أ ب جـ)
- مشترك
ينتج أن:
- ق( جـ) = ق ( ء)
- ب ء = جـ أ
- أ ء = ب جـ
[جـ] .JPG)
غير متطابقان الشروط غير كافية.
[د] .JPG)
غير متطابقان الشروط غير كافية.
[هـ] .JPG)
غير متطابقين.
[و] .JPG)
غير متطابقان الشروط غير كافية.
[ز] .JPG)
غير متطابقان
الشروط غير كافية.
[حـ] .JPG)
غير متطابقان الشروط غير كافية.
٤) ادرس معطيات المثلثين أ ب جـ، س ص ع. إذا كانت المعطيات كافية للتحقق من تطابق المثلثين اكتب <<تطابق مثلثين>>. وبين حالة التطابق. وإذا كانت المعطيات غير كافية للتحقق من تطابق المثلثين اذكر السبب.
[أ] أ ب = ص س، أ جـ = س ع، أ س.
تطابق المثلثين
ضلعين وزاوية محصورة بينهما.
[ب] ب جـ = ص ع، ب أ = س ص، ب ع.
المعطيات غير كافية.
[جـ] أ ب = ص ع، ب حـ = ص س، أ جـ = س ع.
تطابق المثلثين.
الأضلاع الثلاث.
[د] أ ب = س ص. جـ أ = ع س. ب ص.
المعطيات غير كافية.
[هـ] ب = ع. جـ س. ب جـ = س ع
تطابق المثلثين
زاويتين وضلع مرسوم بينهم.
[و] أ س. ب ص. أ جـ = ص ع.
المعطيات غير كافية.
٥) ضع علامة (✔) أمام العبارة الصحيحة:
[أ] يتطابق المثلثان إذا ساوت أطوال الأضلاع الثلاثة في إحداهما نظائرها في الآخر.
(✔)
[ب] يتطابق المثلثان إذا ساوت قياسات الزوايا الثلاث في إحداهما نظائرها في الآخر.
(×)
[جـ] يتطابق المثلثان القائما الزاوية إذا ساوى في أحدهما طولا ضلعين نظيرهما في الآخر.
(×)
[د] يتطابق المثلثان القائما الزاوية إذا ساوى في أحدهما طول الوتر وقياس زاوية أخرى غير القائمة نظائرهما في الآخر.
(✔)
[هـ] يتطابق المثلثان القائما الزاوية إذا ساوى في أحدهما طول الوتر وطول ضلع نظيرتهما في الآخر.
(✔)
٦) [أ] ارسم المثلث الذي فيه قياسات زواياه ٥٠°، ٦٠°، ٧٠°
[ب] هل تستطيع رسم مثلث آخر قياسات زواياه هي ٥٠°، ٦٠°، ٧٠°، لكن لا يطابق المثلث المرسوم في (أ)
ممكن.

.JPG)
.JPG)
.JPG)