الدرس الرابع: التوازي
١) أكمل ما يلي:
[أ] المستقيم العمودي على أحد مستقيمين متوازيين يكون ..... على الآخر.
عمودياً
[ب] إذا وازي مستقيمان مستقيما ثالثاً كان هذان المستقيمان ......
متوازيان
[جـ] إذا قطع مستقيم مستقيمين متوازيين فإن:
(١) كل زاويتين متبادلتين ..... في القياس.
متساويتين
(٢) كل زاويتين متناظرتين ...... في القياس.
متساويتين
(٣) كل زاويتين داخليتين وفي جهة واحدة من القاطع.
متكاملتان
[د] يتوازى المستقيمان إذا قطعهما مستقيم ثالث وحدثت إحدى الحالات الآتية:
(١) زاويتان ..... متساويتان في القياس.
متبادلتان.
(٢) زاويتان .... متساويتان في القياس.
متناظرتان
(٣) زاويتان ...... وفي جهة واحدة من القاطع متكاملتان.
داخليتان
[هـ] إذا تقاطع مستقيمان فإن كل زاويتين متقابلتين بالرأس تكونان .... في القياس.
متساويتان
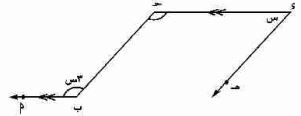
[و] في الشكل المقابل:
إذا كان: // ، // قاطع لهما.
فإن: س = .....°
الزاوية حـ = ٣س بالتبادل الداخلي مع الزاوية ب
إذاً الزاوية ء = ٣س
س + ٣ = ١٨٠°
٤س = ١٨٠°
س = ٤٥°
٢) في الشكل المقابل: قاطع لهما
[أ] أوجد الزوايا التي تساوي في القياس هـ س ب
أ س ص بالتبادل بالرأس، س ص ء بالتناظر
[ب] أوجد الزوايا التي تساوي في القياس س ص حـ
أ س هـ بالتناظر، ص س ب بالتبادل، و ص ء بالتبادل
٣) في الشكل المقابل: ، أوجد قيمة المقدار: س + ص + ع
(إرشاد ارسم خطاً مستقيماً يمر بالنقطة حـ موازياً )
نرسم خطاً مستقيماً
١٨٠° + ١٨٠° = ٣٦٠°
٤) أوجد قيمة س في كل من الأشكال الآتية:
[أ] .JPG)
س = ٦٠°
[ب] .JPG)
س = ٧٥ + ٦٥ = ١٤٠°
[جـ] .JPG)
س = ٢٥ + ٢٠ = ٤٥°
[د] .JPG)
س = ١٠٠°
[هـ] .JPG)
س + ٤٠ = ٦٠
س = ٢٠°
[و] .JPG)
س = ٨٠°
٥) في الشكل المقابل: ق ( س ص ف) = ق ( ع) = ق ( ك) = ق ( م).
اكتب أربعة أزواج من المستقيمات المتوازية. مع ذكر السبب.
ف ص // ك ع
ص ع // ك م
ف ص // ن م
ن م // ك ع
٦) في كل شكل من الأشكال الآتية: أوجد أزواج المستقيمات المتوازية.
[أ] .JPG)
[ب] .JPG)
ب أ // ص س، ء حـ // و هـ


.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)