الدرس الثاني: أوضاع نقطة ومستقيم ودائرة بالنسبة لدائرة

١) أكمل ما يأتي:

أ) إذا كان طول قطر الدائرة ٨ سم، المستقيم ل يبعد عن مركزها ٤ سم، فإن ل يكون .....

مماس للدائرة

ب) إذا كان سطح الدائرة م $\cap$ سطح الدائرة ن = {أ} فإن الدائرتين م، ن تكونان .....

متماستين من الخارج.

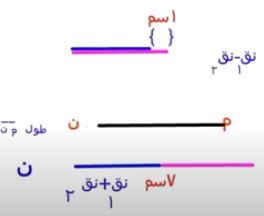
جـ) م، ن دائرتان متقاطعتان، طولا نصفي قطريهما ٣سم، ٤سم على الترتيب، فإن: م ن $\in$ ......

نق_١ - نق_٢ < م ن < نق_١ + نق_٢

]١، ٧[

د) إذا كانت مساحة الدائرة م = ١٦ $\mathrm{\pi }$ سم^٢، أ نقطة في مستويها حيث م أ = ٨ سم، فإن أ تقع ....... الدائرة م

فإن أ تقع خارج الدائرة

هـ) دائرة م طول قطرها ٦ سم، فإذا كان المستقيم ل يقع خارج الدائرة، فإن بعد مركز الدائرة عن المستقيم ل $\in$ .......

و) دائرة طول قطرها (٢س + ٥) سم، المستقيم ل يبعد عن مركزها مسافة (س + ٢) سم فإن المستقيم ل يكون ......

قاطع للدائرة في نقطتين.

٢) في الشكل المقابل: م، ن دائرتان متقاطعتان في أ، ب طولا نصفي قطريهما ٨ سم، ٦ سم على الترتيب، س ص = ٤سم. ادرس الشكل ثم أجب عن الأسئلة الآتية:

أ) أكمل: ص م = .... سم، جـ س = ..... سم، جـ ء = ..... سم

ص م = ٤، جـ = ٨، جـ ء = ١٠ سم.

ب) هل محيط المثلث أ ن م = طولا $\overline{\mathrm{جـ} ء}$؟ فسر إجابتك.

معك لأن أ ن = جـ ن ، أ م = م د

جـ) ما قياس زاوية ن أ م؟

٩٠° لأن (ن م)^٢ = (أ ن)^٢ + (أ م)^٢

١٠٠ = ٣٦ + ٦٤

د) أوجد مساحة المثلث ن أ م.

مـ $△$ = $\frac{\mathrm{١}}{\mathrm{٢}}$ × ٦ × ٨ = ٢٤

هـ) ما طول الوتر المشترك $\overline{أ ب}$؟

أ هـ × ن م= أ ن × أ م

أ هـ × ١٠ = ٦ × ٨

أ هـ = ٤,٨

أ ب = ٩,٦

٣) في الشكل المقابل: $\underset{أ ب}{\leftarrow }$ مماس للدائرة م عند أ، م أ = ٨ سم، ق ($\angle$ أ ب م) = ٣٠°. أوجد طول كل من $\overline{أ ب}$، $\overline{أ \mathrm{جـ}}$

$\because$ أ ب مماس لدائرة، م أ نصف قطر $\therefore$ < م أ ب = ٩٠°

في $△$ أ م ب القائم، طول الضلع أ م المقابل للزاوية ٣٠ = نصف طول الوتر م ب

$\therefore$ م ب = ١٦ سم.

(أ ب)^٢ = (م ب)^٢ - (أ م)^٢ = ٢٥٦ - ٦٤ = ١٩٢

أ ب = ٨ $\sqrt{\mathrm{٣}}$

في $△$ أ جـ ب القائم، طول الضلع أ جـ المقابل للزاوية ٣٠ = نصف طول الوتر أ ب

أ جـ = ٤ $\sqrt{\mathrm{٣}}$

٤) في الشكل المقابل: م، ن دائرتان متقاطعتان في أ، ب، جـ $\in$ $\underset{ب أ}{\leftarrow }$، ء $\in$ الدائرة ن، ق ($\angle$ م ن ء) = ١٢٥°، ق ($\angle$ ب جـ ء) = ٥٥° أثبت أن: $\overleftrightarrow{\mathrm{جـ} ء}$ مماس للدائرة م عند ء.

خط المركزين م ن عمودي على الوتر المشترك أ ب

$\therefore$ الزاوية بينهما = ٩٠

$\because$ مجموع زوايا الاشكل الرباعي الداخلية = ٣٦٠°

$\therefore$ ق ($\angle$ د) = ٣٦٠ - (١٢٥ + ٩٠ + ٥٥) = ٩٠°

$\therefore$ جـ ء مماس للدائرة ن عند ء

٥) $\overline{أ ب}$ قطر في الدائرة م، $\overleftrightarrow{أ \mathrm{جـ}}$، $\overleftrightarrow{ب ء}$، مماسان للدائرة م، $\underset{\mathrm{جـ} م}{\leftarrow }$ قطع الدائرة م في س، ص و يقطع $\overleftrightarrow{ب ء}$ في هـ أثبت أن: جـ س = ص هـ.

$\because$ أ جـ، ب د مماسان للدائرة م من طرفي القطر أ ب

$\therefore$ $\angle$ جـ أ م = $\angle$ هـ، ب م = ٩٠°

$\angle$ أ م جـ = $\angle$ ب م هـ بالتقابل بالرأس

أ م = ب م = نق

$\therefore$ $△$ $△$ أ م جـ، ب م هـ متطابقان وينتج أن

م جـ = م هـ (١)

لكن م س = م ص = نق (٢)

بطرح ٢ من ١ ينتج

جـ س = ص هـ

٦) م، ن دائرتان متقاطعتان في أ، ب، مأ = ١٢ سم، ن أ = ٩ سم، م ن = ١٥ سم. أوجد طول $\overline{أ ب}$.

في $△$ أ م ن

(م ن)^٢ = (١٥)^٢ = ٢٥٥ ، (أ م)^٢ = ١٤٤، (أ ن)^٢ = ٨١

$\because$ ٢٢٥ = ١٤٤ + ٨١

$\therefore$ (م ن)^٢ = (أ م)^٢ + (أ ن)^٢

$\therefore$ $\angle$ م أ ن = ٩٠°

$\because$ خط المركزين $\perp$ الوتر المشترك

$\therefore$ $\angle$ أ س م = ٩٠°

$\therefore$ أ س × م ن = أ م × أ ن

أ س × ١٥ = ١٢ × ٩

$\therefore$ أ س = ٧,٢ سم.

أ ب = ١٤,٤ سم.