تمارين عامة

١) ضع الرمز المناسب $\in$ أو $\notin$ أو $\subset$ أو $\bcancel{\subset }$ مكان النقط:

أ) ٨ .... {٥، ٧}

$\notin$

ب) {٣} .... {١، ٣، ٢}

$\subset$

جـ) ٢ ..... {٢٢، ٤٤}

$\notin$

د) {١، ٢} ..... مجموعة الأعداد الأولية.

$\bcancel{\subset }$

هـ) $\varnothing$ ..... {٠}

$\subset$

و) (س $\cap$ ص) ..... س

$\subset$

٢) أكمل لتحصل على عبارة صحيحة:

أ) إذا كانت س = {٢، ٣}، ص = {٣، ٥} فإن س $\cap$ ص = ....

{٣}

ب) إذا كانت {١، س} = {٢، ص} فإن س = .....، ص = .....

س = ٢، ص = ١

جـ) إذا كانت س $\subset$ ص فإن س $\cup$ ص = .....، ص = .....

س $\cup$ ص = ص

ص = س

د) {١، ٢، ٤} - {٢، ٤، ٦} = .....

{١}

هـ) إذا كانت ٤ $\in$ {٢، س، ٧} فإن س = .....

س = ٤

٣) اختر الإجابة الصحيحة من بين الإجابات التي بين القوسين أمام كل عبارة.

أ) {١، ٧} ...... {٠، ١، ٢، ٣، ٤.....} ($\in$ أو $\notin$ أو $\subset$ أو $\bcancel{\subset }$ )

$\subset$

ب) س - س = ...... ($\varnothing$ أو صفر أن {٠} أو {١})

$\varnothing$

جـ) إذا كانت {٢، ٥، ٧} = {٥، أ، ٢} فإن أ = .... (٢ أو ٥ أو ٧ أو ٠)

٧

د) {٥} - {١، ٢، ٥} = ..... ({٥} أو {١، ٢} $\varnothing$ أو {١، ٢، ٥})

$\varnothing$

هـ) عدد المجموعات الجزئية لمجموعة {٥} هي .... (٠ أو ١ أو ٢ أو ٣)

$\varnothing$، {٥}

٤) إذا كانت ش = {١، ٢، ٣، ٤، ٥، ٦}، س = {٢، ٣، ٥}، ص = {٣، ٤، ٥} مثل هذه المجموعات بشكل فن، ثم اكتب بطريقة السرد كلاً من: س $\cup$ ص، س $\cap$ ص، س - ص، سَ

س $\cup$ ص = {٢، ٣، ٥، ٤}، س $\cap$ ص = {٣، ٥}

س - ص = {٢}، سَ = {١، ٤، ٦}

٥) عبر عن الجزء الملون في كل من الأشكال التالية:

٦) باستخدام شكل فن المقابل. أوجد بطريقة السرد كلاً من:

أ) س $\cup$ ص

{٣، ١، ٢، ٤، ٨، ٩}

ب) س $\cap$ ص

{١، ٢}

جـ) س - ص

{٣}

د) صَ

{٥، ٣}

هـ) (س $\cup$ ص)َ

{٥}

٧) اكتب جميع المجموعات الجزئية للمجموعة س = {أ، ب، جـ}

$\varnothing$، {أ}، {ب}، {جـ}، {أ، ب}، {ب، جـ}، {أ، جـ}، {أ، ب، جـ}

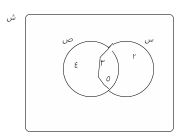
٨) باستخدام شكل فن المقابل. اكتب بطريقة السرد كلاً من:

أ) س $\cap$ ع

{٥}

ب) س - ص

{٤، ٥، ٣}

جـ) ص - ع

ص

د) س $\cup$ ع

{٢، ٤، ٣، ٥، ٦، ٧}

هـ) ع - س

{٦، ٧}

و) سَ

{١، ٦، ٧، ٨}

٩) إذا كانت س = {٣، ٤، ٥}، ص = {٢، ٣، ٤} ضع الرمز المناسب $\in$ أو $\notin$ أو $\subset$ أو $\bcancel{\subset }$ مكان النقط:

أ) ٢ ..... س

$\notin$

ب) {٣، ٥} ...... س $\cap$ ص

$\bcancel{\subset }$

جـ) {٣، ٢} ...... س $\cup$ ص

$\subset$

د) ٥ ..... س - ص

$\notin$

هـ) $\varnothing$ .... ص

$\subset$

و) {٢، ٣، ٤} ..... س

$\bcancel{\subset }$

١٠) أوجد قيمة س التي تجعل العبارة صحيحة:

أ) ٣ $\in$ {٥، ٧، س +١}

س = ٢

ب) س $\in$ {٢، ٥} $\cap$ {٣، ٥}

{٥}

جـ) {٢، س} $\cap$ {٣، ٧} = {٣}

س = ٣

١١) اكتب ما يمثله الجزء الملون في كل من أشكال فن التالية:

١٢) أوجد جميع المجموعات الجزئية للمجموعة س = {أ، ب، جـ، د} التي عدد عناصر كل منها = ٢كم عدد هذه المجموعات.

{أ، ب}، {ب، جـ}، {جـ، ء}، {أ، ء}، {ب، ء}، {أ، جـ}

عدد المجموعات = ٦ مجموعات