الدرس الثالث: الدالة التطبيق
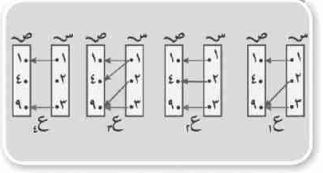
١) أي من العلاقات التالية تمثل دالة من س إلى ص؟ وإذا كانت العلاقة تمثل دالة، فأوجد مدى الدالة.
العلاقة الأولى: دالة، المدى المجموعة {١، ٩}
العلاقة الثانية: دالة، المدى المجموعة {١، ٤، ٩}
العلاقة الثالثة: ليست دالة
العلاقة الرابعة: ليست دالة
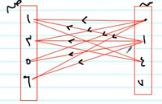
٢) أي من العلاقات التالية تمثل دالة من س إلى ص؟ وإذا كانت العلاقة تمثل دالة، فأوجد مدى الدالة.
العلاقة (١): دالة، المدى: {١، ٢، ٣، ٤}
العلاقة (٢): ليست دالة
العلاقة (٣): دالة، المدى: {١، ٢، ٣، ٤، ٥}
٣) إذا كانت س = {٢، ٥، ٨}، ص = {١٠، ١٦، ٢٤، ٣٠} وكانت ع علاقة من س إلى ص حيث أ ع ب تعني ((أ عامل من عوامل ب)) لكل أ س، ب ص اكتب بيان ع ومثلها بمخطط سهمي وآخر بياني. هل ع دالة؟ ولماذا؟
المخطط السهمي:
ع = {(٢، ١٠)، (٢، ١٦)، (٢، ٢٤)، (٢، ٣٠)، (٥، ١٠)، (٥، ٣٠)، (٨، ١٦)، (٨، ٢٤)}
ليست دالة. لأن العنصر٢ س يخرج منه سهمين، العنصر٥ س يخرج منه سهمين، العنصر ٨ س يخرج منه سهمين.
المخطط البياني:
٤) إذا كانت س = {٠، ١، ٤، ٧}، ص = {١، ٢، ٥، ٦}، ع علاقة من س إلى ص حيث أ ع ب تعني ((أ + ب < ٨)) لكل أ س، ب ص اكتب بيان ع ومثلها بمخطط سهمي وآخر بياني. هل ع دالة؟ ولماذا؟
س = {٠، ١، ٤، ٧} أ
ص = {١، ٢، ٥، ٦} ب
أ + ب < ٨
بيان ع = {(٠، ١)، (٠، ٣)، (٠، ٥)، (٠، ٦)، (١، ١)، (١، ٣)، (١، ٥)، (١، ٦)، (٤، ١)، (٤، ٣)}
ع ليست دالة لأن العنصر ١ ظهر كمسقط أول أكثر من مرة.
المخطط السهمي:
المخطط البياني:
٥) إذا كانت س = {١، ٢، ٤، ٦، ١٠}، وكانت ع علاقة على س حيث أ ع ب تعني ((أ مضاعف ب)) لكل أ، ب س اكتب بيان ع ومثلها بمخطط سهمي وآخر بياني. هل ع دالة؟ ولماذا؟
س = {١، ٢، ٤، ٦، ١٠} أ
س = {١، ٢، ٤، ٦، ١٠} ب
أ مضاعف ب "يقبل القسمة على ب"
بيان ع = {(١، ١)، (٢، ١)، (٢، ٢)، (٤، ١)، (٤، ٢)، (٤، ٤)، (٦، ١)، (٦، ٢)، (٦، ٦)، (١٠، ١)، (١٠، ٢)، (١٠، ١٠)}
ع ليست دالة لأن العنصر ١ ظهر كمسقط أول أكثر من مرة.
المخطط السهمي:
المخطط البياني:
٦) إذا كانت س = {١، ٢، ٣، ٦، ١١}، وكانت ع علاقة على س حيث أ ع ب تعني ((أ + ٢ب = عدد فردي)) لكل أ، ب س اكتب بيان ع ومثلها بمخطط سهمي وآخر بياني. هل ع دالة؟ ولماذا؟
س = {١، ٢، ٣، ٦، ١١} أ
س = {١، ٢، ٣، ٦، ١١} ب
أ + ٢ب = عدد فردي
بيان ع = {(١، ١)، (١، ٢)، (١، ٣)، (١، ٦)، (١، ١١)، (٣، ١)، (٣، ٢)، (٣، ٦)، (٣، ٣)، (٣، ١١)، (١١، ١)، (١١، ٢)، (١١، ٣)، (١١، ٦)، (١١، ١١)}
ع ليست دالة لأن العنصر ٢ ظهر كمسقط مرة واحدة فقط.

.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)