اختبار الوحدة الأولى
١) إذا كانت س = {٠، ١، ٤، ٧}، ص = {١، ٣، ٥، ٦}، ع علاقة من س إلى ص، حيث أ ع ب تعني: ((أ + ب < ٦)) لكل أ س، ب ص اكتب بيان ع ومثلها بمخطط سهمي وآخر بياني. هل ع دالة؟ اذكر السبب.
س = {٠، ١، ٤، ٧} (أ)
ص = {١، ٣، ٥، ٦} (ب)
أ + ب < ٦
بيان ع = {(٠، ١)، (٠ ٢)، (٠، ٥)، (١، ١)، (١، ٣)، (٤، ١)}
ع ليست دالة لأن العنصر ٧ لم يظهر كمسقط أول مرة واحدة في بيان ع.
٢) مثل بيانياً كلاً من الدوال الآتية:
أ) د (س) = ٣س - ١
د (١) = ٣ × ١ - ١ = ٢
د (٢) = ٣ × ٢ - ١ = ٥
د (٣) = ٣ × ٣ - ١ = ٨
| س | ١ | ٢ | ٣ |
| ص | ٢ | ٥ | ٨ |
ب) د (س) = - ٢س
| س | ١ | ٢ | ٣ |
| ص | -٢ | -٤ | -٦ |
د (١) = -٢ (١) = -٢
د (٢) = -٢ (٢) = -٤
د (٣) = -٢ (٣) = -٦
جـ) د (س) = س٢ - ٣ متخذاً س [-٣، ٣]
| س | -٣ | -٢ | -١ | ٠ | ١ | ٢ | ٣ |
| ص | ٦ | ١ | -٢ | -٣ | -٢ | ١ | ٦ |
نقطة رأس المنحني = (٠، -٣)
معادلة محور تماثل س = ٠
القيمة الصغرى -٣
د) د (س) = ١ - ٣س + س متخذاً س٢ [-١، ٤]
| س | -١ | ٠ | ١ | ٢ | ٣ | ٤ |
| ص | ٥ | ١ | -١ | -١ | ١ | ٥ |
نقطة رأس المنحني (، )
معادلة محور التماثل س =
القيمة الصغرى =
س = = ١,٥ (ب معامل س، أ معامل س٢)
د (١,٥) = ١ - ٣ × ١,٥ + (١,٥)٢
= (- ٤,٥ + ٢,٢٥)
=
٣) أثناء قراءة كريم لكتاب وجد أنه بعد ٣ ساعات تبقى له ٥٠ صفحة، وبعد ٦ ساعات تبقى له ٢٠ صفحة. فإذا كانت العلاقة بين الزمن (ن) وعدد الصفحات (ص) هي علاقة خطية:
أ) مثل العلاقة بين ن، ص بيانياً ثم أوجد العلاقة الجبرية بينهما.
(٣، ٥٠)، (٦، ٢٠)
(٠، ٨٠)، (٨، ٠)
ص = أ س + ب
(٠، ٨٠) تحقق العلاقة
٨٠ = أ × ٠ + ب ب = ٨٠
ص = أ س + ٨٠
(٨، ٠) تحقق العلاقة
٠ = أ × ٨ + ٨٠
٨ أ + ٨٠ = ٠
أ =
أ = - ١٠
العلاقة بين الزمن ن = -١٠ص + ٨
ب) ما الوقت الذي ينتهي فيه كريم من قراءة الكتاب؟
بعد ٨ ساعات.
جـ) كم عدد صفحات الكتاب المتبقية عندما بدأ كريم القراءة؟
٨٠ صفحة.
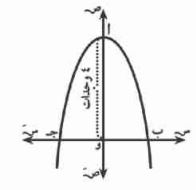
٤) الشكل المقابل: يمثل منحنى الدالة د حيث: د (س) = م - س، إذا كان أ و = ٤ وحدات
أوجد:
أ) قيمة م.
ص = م - س٢
(٠، ٤) لمنحني الدالة
تحقق الدالة
٤ = م - (٠)٢
م = ٤
د (س) = ٤ - س٢
نضع ص = ٠
٠ = ٤ - س٢
س٢ =
س = ٢
ب) إحداثيي ب، جـ
ب (٢، ٠)، جـ (-٢، ٠)
جـ) مساحة المثلث الذي رؤوسه أ، ب، جـ.
مساحة = × طول القاعدة × الارتفاع
= × ٤ × ٤
= ٨ وحدة مربعة.

.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)