الدرس الأول: حل معادلات الدرجة الثانية في متغير واحد
أولاً: الاختيار من متعدد
١) المعادلة: (س - ١) (س + ٢) = ٠ من الدرجة:
أ) الأولى
ب) الثانية
جـ) الثالثة
د) الرابعة
٢) مجموعة حل المعادلة س٢ = س في ح هي:
س٢ - س = ٠
س (س - ١) = ٠
س = ٠،
س -١ = ٠
س = ١
م. ح = {٠، ١}
أ) {٠}
ب) {١}
جـ) {-١، ١}
د) {٠، ١}
٣) مجموعة حل المعادلة س٢ + ٣ = ٠ في ح هي:
س٢ + ٣ = ٠
س٢ = -٣
س =
أ) {-٣}
ب) {}
جـ) {}
د)
٤) مجموعة حل المعادلة س٢ -٢س = -١ في ح هي:
س٢ -٢س + ١ = ٠
(س - ١) (س - ١) = ٠
إما س - ١ = ٠ س = ١
س - ١ = ٠ س = ١
م. ح = {١}
أ) {-١}
ب)
جـ) {-١، ١}
د) {١}
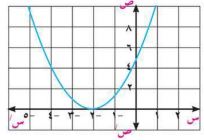
٥) يمثل الشكل المقابل المنحني البياني لدالة تربيعية د.
م. ح المعادلة الإحداثي السيني لنقط تقاطع المنحني مع محور السينات إذاً م . ح {-٢}
أ) {-٢}
ب) {٤}
جـ)
د)
ثانياً: أجب عن الأسئلة الآتية:
٦) أوجد مجموعة حل كل من المعادلات الآتية في ح:
أ) س٢ -١ = ٠
س٢ = ١، س = ١
م. ح = {١، -١}
ب) س٢ +٣س = ٠
س (س + ٣) = ٠
س = ٠
س + ٣ = ٠
س = -٣
م. ح = {٠، -٣}
جـ) (س - ٤)٢ = ٠
نأخذ جذر الطرفين
س - ٤ = ٠
س = ٤
م. ح = {٤}
د) س٢ -٦س + ٩ = ٠
(س - ٣) (س - ٣) = ٠
س = ٣
م. ح = {٣}
هـ) س٢ + ٩ = ٠
س٢ = -٩ مرفوض
م. ح =
و) س (س + ١) (س - ١) = ٠
- إما س = ٠
- أو س + ١
س = -١
- أو س - ١ = ٠
س = ١
م. ح = {٠، -١، + ١}
٧) يبين كل شكل من الأشكال التالية الرسم البياني لدالة من الدرجة الثانية. أوجد مجموعة الحل للمعادلة د (س) = ٠ في كل شكل.
الرسم البياني (أ) م. ح = {-٢}
الرسم البياني (ب) م. ح = {}
الرسم البياني (جـ) م. ح = {١، -٣}
٨) أوجد مجموعة الحل لكل من المعادلات الآتية في ح وحقق الناتج بيانياً:
أ) س٢ = ٣س + ٤٠
ب) ٢س٢ = ٣ - ٥س
جـ) ٦س٢ = ٦ - ٥س
د) (س - ٣)٢ = ٥
هـ) س٢ + ٢س = ١٢
و) س٢ - س = ١
٩) حل المعادلات الآتية في ح باستخدام القانون العام مقرباً الناتج لرقم عشري واحد.
أ) ٣س٢ - ٦٥ = ٠
س = حيث أ س٢ + ب س + جـ = ٠
أ = ٣، ب = صفر، جـ = -٦٥
نعوض القانون.
س = = = ٤,٧
م. ح = {-٤,٧، ٤,٧}
ب) س٢ -٦س + ٧ = ٠
أ = ١، ب = -٦، جـ = ٧
س = =
إما س = = ٤,٤
أو س = = ١,٦
م. ح = {١,٦، ٤,٤}
جـ) س٢ + ٦س + ٨ = ٠
د) ٢س٢ +٣س - ٤ = ٠
هـ) ٥س٢ -٣س - ١ = ٠
و) ٣س٢ - ٦س - ٤ = ٠
١٠) أعداد: إذا كان مجموع الأعداد الصحيحة المتتالية (١ + ٢ + ٣ + .....+ ن) يعطى بالعلاقة جـ = (١ + ن) عدداً صحيحاً متتالياً بدءاً من العدد ١ يكون مجموعهما مساوياً:
أ) ٧٨
ب) ١٧١
جـ) ٢٥٣
د) ٤٦٥
٧٨ = (١ + ن) × ٢
١٥٦ = ن (١ + ن)
١٥٦ = ن + ن٢
ن٢ + ن - ١٥٦ = ٠
(ن - ١٢) (ن + ١٣) = ٠
إما ن - ١٢ = ٠
ن = ١٢
أو ن + ١٣ = ٠
ن = -١٣ مرفوض
الحل ١٢ عدد
١١) يبين كل شكل من الأشكال الآتية الرسم البياني لدالة من الدرجة الثانية في متغير واحد. أوجد قاعدة كل دالة من هذه الدوال.
- المخطط البياني أ) س = ٢، س = -٣
س - ٢ = ٠، س + ٣ = ٠ = د (س)
س٢ + س - ٦ = ٠
د (س) = س٢ + س - ٦
- المخطط البياني ب)
س = ٠، س = -٣
د (س) = س (س + ٣)
د (س) = س + ٣س
- المخطط البياني جـ)
س = ١، س = ٥
س - ١، س - ٥
د (س) = (س - ١) (س - ٥)
د (س) = س٢ - ٦س + ٥
١٢) اكتشف الخطأ: أوجد مجموعة حل المعادلة (س - ٣) = (س - ٣).
أي الحلين صحيح ولماذا؟
إجابة كريم هي الصحيحة.
١٣) تفكير ناقد: قذفت كرة رأسياً إلى أعلى بسرعة (ع) تساوي ٢٩,٤ متر/ث. احسب الفترة الزمنية (ن) بالثانية التي تستغرقها الكرة حتى تصل إلى ارتفاع (ف) متراً، حيث ف تساوي ٣٩,٢ متراً علماً بأن العلاقة بين ف، ن تعطى كالآتي ف = ع ن -٤,٩ ن٢.
ف = ع ن - ٤,٩ ن٢ (نقسم على -٤,٩)
-٨ = -٦ن + ن٢
ن٢ - ٦ن + ٨ = ٠
(ن - ٢) (ن - ٤) = ٠
ن - ٢ = ٠، ن = ٢
ن - ٤ = ٠، ن = ٤

.JPG)
.JPG)
.JPG)
.JPG)
