الدرس الأول: التباين

١) في الشكل المقابل:

أ ب جـ مثلث فيه أ جـ > أ ب، س $\in$ $\overline{أ ب}$

ص $\in$ $\overline{أ \mathrm{جـ}}$ بحيث ق ($\angle$ أ س ص) = ق ($\angle$ أ ص س)

أثبت أن: ص جـ > س ب

في $△$ أ س ص

$\because$ ق ($\angle$ أ س ص) = ق ($\angle$ أ ص س) $\therefore$ أ ص = أ س

أ جـ > أ ب ، أ س = أ ص

إذاً ص جـ > س ب

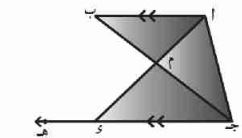
٢) في الشكل المقابل: $\overline{أ ب}$ // $\underset{\mathrm{جـ} ء}{\leftarrow }$، $\overline{أ ء}$ $\cap$ $\overline{\mathrm{جـ} ب}$ = {م}، هـ $\in$ $\underset{\mathrm{جـ} ء}{\leftarrow }$، هـ $\notin$ $\overline{\mathrm{جـ} ء}$

أثبت أن:

أ) ق ($\angle$ أ جـ ء) > ق ($\angle$ أ ب جـ)

$\because$ $\overline{أ ب}$ // $\underset{\mathrm{جـ} ء}{\leftarrow }$، $\overline{ب \mathrm{جـ}}$ قاطع

$\therefore$ ق ($\angle$ ب) = ق ($\angle$ ء جـ ب) بالتبادل (١)

ق ($\angle$ ء جـ ب) + ق ($\angle$ أ جـ ب) > ق ($\angle$ ب)

$\therefore$ ق ($\angle$ أ جـ ء) > ق ($\angle$ أ جـ ب)

ب) ق ($\angle$ أ ء هـ) > ق ($\angle$ أ ب جـ)

$\because$ $\angle$ أ ء هـ خارجة عن المثلث أ جـ ء

$\therefore$ ق ($\angle$ أ ء هـ) > ق ($\angle$ أ جـ ء)

ق ($\angle$ ء) > ق ($\angle$ جـ)

ق ($\angle$ جـ) > ق ($\angle$ ب)

$\therefore$ ق ($\angle$ أ ء هـ) > ق ($\angle$ أ ب جـ)

٣) م نقطة داخل المثلث أ ب جـ،

أثبت أن: ق ($\angle$ أ م ب) > ق ($\angle$ أ جـ ب)

العمل: نرسم $\underset{أ م}{\leftarrow }$ يقطع $\overline{ب \mathrm{جـ}}$ في س

$\because$ $\angle$ ٣ خارجة عن $△$ م س ب

$\therefore$ ق ($\angle$ ٣) > ق ($\angle$ ٢)

$\because$ $\angle$ ٢ خارجة عن $△$ أ س جـ

$\therefore$ ق ($\angle$ ٢) > ق ($\angle$ ١)

$\therefore$ ق ($\angle$ ٣) > ق ($\angle$ ١)