نموذج امتحانات الجبر والإحصاء النموذج الأول

١) أكمل ما يأتي:

(١) مجموعة حل المعادلة (س^٢ + ٣) (س^٣ + ١) = ٠ هي ..... (س $\in$ ح)

• (س^٢ + ٣)

س^٢ + ٣ = ٠

س^٢ = -٣

س = $\sqrt{-\mathrm{٣}}$

• (س^٣ + ١) = ٠

س^٣ + ١ = ٠

س^٣ = - ١

س = $\sqrt[\mathrm{٣}]{-\mathrm{١}}$

الجواب: {- ١}

(٢) إذا كان الحد الأدنى لمجموعة هو ١٠ والحد الأعلى لها هو س ومركزها هو ١٥ فإن س = .......

س = ٢٠

(٣) ]-٢، ٢] $\cup$ {-٢، ٠} = ........

[-٢، ٢]

(٤) المكعب الذي حجمه ٨ سم^٣ يكون مجموع أطوال أحرفه = ....... سم

٢٤

(٥) المعكوس الضربي للعدد $\sqrt{\mathrm{٣}}+\sqrt{\mathrm{٢}}$ = ....... في أبسط صورة.

$\frac{\mathrm{١}}{\sqrt{\mathrm{٣}}+\sqrt{\mathrm{٢}}}\times \frac{\sqrt{\mathrm{٣}}-\sqrt{\mathrm{٢}}}{\sqrt{\mathrm{٣}}-\sqrt{\mathrm{٢}}} = \frac{\sqrt{\mathrm{٣}}-\sqrt{\mathrm{٢}}}{\mathrm{٣} - \mathrm{٢}}=\frac{\sqrt{\mathrm{٣}}-\sqrt{\mathrm{٢}}}{\mathrm{١}}$ = $\sqrt{\mathrm{٣}}-\sqrt{\mathrm{٢}}$

٢) اختر الإجابة الصحيحة من بين الإجابات المعطاة:

(١) إذا كان نصف قطر كرة = ٦ سم فإن حجمها يساوي: (أ) ٦ $\mathrm{\pi }$ سم^٣، (ب) ٣٦$\mathrm{\pi }$ سم^٣، (جـ) ٧٢ $\mathrm{\pi }$ سم^٣، (ء) ٢٨٨ $\mathrm{\pi }$ سم^٣

$\frac{\mathrm{٤}}{\mathrm{٣}}\mathrm{\pi }$ نق^٣ = $\frac{\mathrm{٤}}{\mathrm{٣}}\mathrm{\pi }$ ٢١٦ (ء) ٢٨٨ $\mathrm{\pi }$ سم^٣

(٢) إذا كانت النقطة (أ، ١) تحقق العلاقة س + ص = ٥ فإن أ = ........ (أ) ١، (ب) -٤، (جـ) ٤، (ء) ٥

(جـ) ٤

(٣) (٢$\sqrt[\mathrm{٣}]{\mathrm{٢}}$)^٣ = ...... (أ) ٤، (ب) ٨، (جـ) ١٦، (ء) ٤٠

(٢$\sqrt[\mathrm{٣}]{\mathrm{٢}}$)^٣ = ٨ × ٢ = (جـ) ١٦

(٤) الوسيط لمجموعة من القيم ٣٤، ٢٣، ٢٥، ٤٠، ٢٢، ٤ هو (أ) ٢٢، (ب) ٢٣، (جـ) ٢٤، (ء) ٢

٤، ٢٢، ٢٣، ٢٥، ٣٤، ٤٠

$\frac{\mathrm{٢٣} + \mathrm{٢٥}}{\mathrm{٢}}=\frac{\mathrm{٤٨}}{\mathrm{٢}}$ =٢٤، (جـ) ٢٤

(٥) إذا كان الوسط الحسابي للقيم ٢٧، ٨، ١٦، ٢٤، ٦، ك هو ١٤ فإن ك تساوي: (أ) ٣، (ب) ٦، (جـ) ٢٧، (ء) ٨٤

$\frac{\mathrm{٢٨} + \mathrm{٨} + \mathrm{١٦} + \mathrm{٢٤} + \mathrm{٦} + ك}{\mathrm{٦}}$ = ١٤

$\frac{\mathrm{٨١} + ك}{\mathrm{٦}}$ = ١٤

٨١ + ك = ٨٤

ك = ٨٤ - ٨١ = ٣

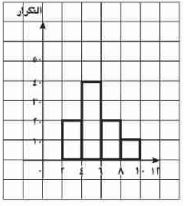
(٦) في الشكل المقابل: قيمة المنوال = ...... (أ) ٤، (ب) ٥، (جـ) ٦، (ء) ٤٠

(ب) ٥

٣) (أ) أوجد قيمة: $\sqrt{\mathrm{١٨}}$ + $\sqrt{\mathrm{٥٤}}$ - ٣$\sqrt{\mathrm{٢}}$ - $\frac{\mathrm{١}}{\mathrm{٢}}\sqrt{\mathrm{٢٤}}$

$\sqrt{\mathrm{٩} \times \mathrm{٢}} + \sqrt{\mathrm{٩} \times \mathrm{٦}}-\mathrm{٣}\sqrt{\mathrm{٢}}-\frac{\mathrm{١}}{\mathrm{٢}}\sqrt{\mathrm{٤} \times \mathrm{٦}}$

$\bcancel{\mathrm{٣}\sqrt{\mathrm{٢}}}+\mathrm{٣}\sqrt{\mathrm{٦}}\bcancel{-\mathrm{٣}\sqrt{\mathrm{٢}}}-\sqrt{\mathrm{٦}}=\mathrm{٢}\sqrt{\mathrm{٦}}$

(ب) إذا كان س = $\frac{\mathrm{٣}}{\sqrt{\mathrm{٥}}-\sqrt{\mathrm{٢}}}$، ص = $\sqrt{\mathrm{٥}}-\sqrt{\mathrm{٢}}$ أثبت أ س، ص عددان مترافقان

س = $\frac{\mathrm{٣}}{\sqrt{\mathrm{٥}}-\sqrt{\mathrm{٢}}}$ × $\frac{\sqrt{\mathrm{٥}}+\sqrt{\mathrm{٢}}}{\sqrt{\mathrm{٥}}+\sqrt{\mathrm{٢}}}=\frac{\mathrm{٣}(\sqrt{\mathrm{٥}}+\sqrt{\mathrm{٢}})}{\mathrm{٥} - \mathrm{٢}}$

س = $\frac{\mathrm{٣}(\sqrt{\mathrm{٥}}+\sqrt{\mathrm{٢}})}{\mathrm{٣}}=\sqrt{\mathrm{٥}}+\sqrt{\mathrm{٢}}$

ص = $\sqrt{\mathrm{٥}}-\sqrt{\mathrm{٢}}$

س، ص عددان مترافقان.

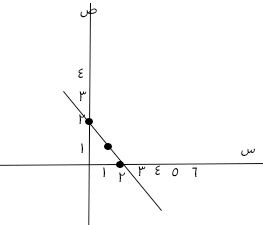
٤) (أ) ارسم بيانياً العلاقة الخط ية ص = ٢ - س

ص = ٢ - س

عندما س = ٠، ص = ٢ - ٠ = ٢ (٠، ٢)

عندما س = ١، ص = ٢ - ١ = ١ (١، ١)

عندما س = ٢، ص = ٢ - ٢ = ٢ (٢، ٠)

(ب) أوجد مجموعة حل المتباينة: $\frac{\mathrm{٣}س + \mathrm{١}}{\mathrm{٦}}$ < س + ١ < $\frac{س + \mathrm{٤}}{\mathrm{٢}}$ في ح ومثلها على خط الأعداد.

٦ × $\frac{\mathrm{٣}س + \mathrm{١}}{\mathrm{٦}}$ < ٦ × (س + ١) < $\frac{س + \mathrm{٤}}{\mathrm{٢}}$ × ٦

٣س + ١ < ٦س + ٦ < ٣س + ١٢

٣س + ١ - ٦ < ٦س < ٣س + ١٢ - ٦

٣س - ٥ < ٦س < ٣س + ٦ بطرح ٣س

٣س - ٥ - ٣س < ٦س - ٣س < ٣س + ٦ - ٣س

-٥ < ٣س < ٦ نقسم على ٣

$\frac{-\mathrm{٥}}{\mathrm{٣}}$ <$\frac{\mathrm{٣}}{\mathrm{٣}}$ س < $\frac{\mathrm{٦}}{\mathrm{٣}}$

$\frac{-\mathrm{٥}}{\mathrm{٣}}$ < س < ٢

م. ح = ]$\frac{-\mathrm{٥}}{\mathrm{٣}}$، ٢[

٥) (أ) أسطوانة دائرية قائمة طول ن صف قطر قاعدتها ٤ $\sqrt{\mathrm{٢}}$ سم وارتفاعها ٩ سم. أوجد حجمها بدلالة $\mathrm{\pi }$. وإذا كان حجمها يساوي حجم كرة فأوجد طول نصف قطر الكرة

حجم الأسطوانة = $\mathrm{\pi }$ نق^٢ ع = $\mathrm{\pi }$ × (٤$\sqrt{\mathrm{٢}}$) × ٩

= $\mathrm{\pi }$ × ١٦ × ٢ × ٩

= ٢٨٨ $\mathrm{\pi }$ سم^٣.

حجم الكرة = $\frac{\mathrm{٤}}{\mathrm{٣}}$ $\mathrm{\pi }$ نق^٣

٢٨٨ $\bcancel{\mathrm{\pi }}$ = $\frac{\mathrm{٤}}{\mathrm{٣}}$ $\bcancel{\mathrm{\pi }}$ نق^٣

٢٨٨ = $\frac{\mathrm{٤}}{\mathrm{٣}}$ × نق^٣

$\frac{\mathrm{٣}}{\mathrm{٤}}$ × ٢٨٨ = $\frac{\mathrm{٤}}{\mathrm{٣}}$ × نق^٣ × $\frac{\mathrm{٣}}{\mathrm{٤}}$

٢١٦ = نق^٣

نق = ٦

(ب) أوجد الوسط الحسابي للتوزيع التكراري الآتي:

الوسط الحسابي = $\frac{\mathrm{مج} (م \times ك)}{\mathrm{مج} ك}$ = $\frac{\mathrm{١٥٥٠}}{\mathrm{٥٠}}$ = ٣١