الدرس الثاني: المضلع

١) احسب قياس الزاوية المجهولة في كل مما يأتي:

[أ]

القانون = $\frac{(ن - \mathrm{٢}) \times \mathrm{١٨٠}}{ن}$

س = $\frac{(\mathrm{٥} - \mathrm{٢}) \times \mathrm{١٨٠}}{\mathrm{٥}}$ = ١٠٨°

[ب]

القانون = $\frac{(ن - \mathrm{٢}) \times \mathrm{١٨٠}}{ن}$

ص = $\frac{(\mathrm{٨} - \mathrm{٢}) \times \mathrm{١٨٠}}{\mathrm{٨}}$ = ١٣٥°

س = ١٨٠ - ١٣٥ = ٤٥°

[جـ]

القانون = $\frac{(ن - \mathrm{٢}) \times \mathrm{١٨٠}}{ن}$

٢س = $\frac{(\mathrm{٦} - \mathrm{٢}) \times \mathrm{١٨٠}}{\mathrm{٦}}$ = ١٢٠°

س = ٦٠°

ص = ١٨٠ - ١٢٠ = ٦٠°

ع = ١٨٠ - (٦٠ + ٦٠) = ٦٠°

[د]

القانون = (ن - ٢) × ١٨٠

٨ أ = (٥ - ٢) × ١٨٠ = ٥٤٠

أ = ٦٧,٥

[هـ]

القانون = $\frac{(ن - \mathrm{٢}) \times \mathrm{١٨٠}}{ن}$

ص = $\frac{(\mathrm{٨} - \mathrm{٢}) \times \mathrm{١٨٠}}{\mathrm{٨}}$ = ١٣٥°

س = $\frac{\mathrm{١٣٥}}{\mathrm{٢}}$ = ٦٧,٥

ع = ١٨٠ - ١٣٥ = ٤٥°

[و]

مجموع قياسات الزوايا الداخلة لتشكل الخماسي = (٥ - ٢) × ١٨٠ = ٥٤٠

٣ أ + ١٨٠ = ٥٤٠

٣ أ = ٥٤٠ - ١٨٠

٣ أ = ٣٦٠

أ = ١٢٠

[ز]

أ = ١٨٠ - (٦٢ + ٦٢) = ٥٦°

ب = $\frac{\mathrm{١٨٠} - \mathrm{٥٦}}{\mathrm{٢}}$= ٦٢°

[حـ]

ب = ١٨٠ - (٤٢ + ٩٠) = ٤٨

جـ = ١٨٠ - (٩٠ + ٣٨) = ٥٢°

٢) ارسم الشكل الرباعي أ ب جـ ء في كل من الحالات الآتية:

(١) $\overline{أ ب}$ // $\overline{ء \mathrm{جـ}}$، $\overline{أ ء}$ // $\overline{ب \mathrm{جـ}}$

متوازي أضلاع.

(٢) $\overline{أ ب}$ // $\overline{ء \mathrm{جـ}}$، أ ب = ء جـ

(٣) أ ب = ء جـ، أ ء = ب جـ

(٤) ق ($\angle$ أ) = ق ($\angle$ جـ)، ق ($\angle$ ب) = ق ($\angle$ ء)

(٥) $\overline{أ \mathrm{جـ}}$، $\overline{ب ء}$ ينصف كل منهما الآخر.

مما سبق استنتج الحالات التي يكون فيها الشكل الرباعي متوازي الأضلاع.

٣) أكمل ما يأتي:

(١) المربع هو ..... احدى زوايا قائمة.

معين.

(٢) الشكل الرباعي الذي أضلاعه متساوية في الطول يسمى .....

معين

(٣) متوازي الأضلاع الذي قطراه ..... يسمى مستطيلاً.

متساويان.

(٤) متوازي الأضلاع الذي قطراه متعامدان يكون .... أو ....

المعين أو المربع.

(٥) أ ب جـ ء متوازي الأضلاع فيه ق ($\angle$ أ) = ٥٠° يكون ق ($\angle$ ب) = ....°

ق ($\angle$ أ) + ق ($\angle$ ب) = ١٨٠°

ق ($\angle$ أ) = ق ($\angle$ جـ)

(٦) المستطيل هو .... إحدى زوايا قائمة.

متوازي أضلاع.

(٧) الشكل الرباعي الذي قطراه ينصف كل منهما الآخر يسمى .....

متوازي أضلاع.

(٨) إذا كان أ ب جـ ء معين فإن ..... $\perp$ ....

أ جـ $\perp$ ب ء

(٩) الشكل الرباعي الذي فيه ضلعان متوازيان يسمى .....

شبه منحرف.

(١٠) في متوازي الأضلاع س ص ع ل إذا كان ق ($\angle$ س) = $\frac{\mathrm{١}}{\mathrm{٢}}$ ق ($\angle$ ص) فإن ق ($\angle$ ص) = .....°

ق ($\angle$ س) + ق ($\angle$ ص = ١٨٠°

$\frac{\mathrm{١٨٠}}{\mathrm{٣}}$ × ٢ = ١٢٠

(١١) القطران في .... يصنع كل منهما زاوية قياسها ٤٥° مع الضلع المجاور.

المربع

(١٢) المعين الذي محيطه ٤٢ سم يكون طول ضلعه = ..... سم.

$\frac{\mathrm{٤٢}}{\mathrm{٤}}$ = ١٠,٥

٤) أوجد عدد أضلاع مضلع محدب منتظم قياس إحدى زواياه:

[أ] ١٤٠°

عدد الأضلاع = $\frac{\mathrm{٣٦٠}}{\mathrm{١٨٠} - \mathrm{١٤٠}}=\frac{\mathrm{٣٦٠}}{\mathrm{٤٠}}$ = ٩ أضلاع.

[ب] ١٣٥°

عدد الأضلاع = $\frac{\mathrm{٣٦٠}}{\mathrm{١٨٠} - \mathrm{١٣٥}}=\frac{\mathrm{٣٦٠}}{\mathrm{٤٥}}$ = ٨ أضلاع.

٥) هل للمضلع المنتظم زاوية داخلة قياسها ١٠٠°؟ ولماذا؟

عدد الأضلاع = $\frac{\mathrm{٣٦٠}}{\mathrm{١٨٠} - \mathrm{١٠٠}}=\frac{\mathrm{٣٦٠}}{\mathrm{٨٠}}$ = ٤,٥

لا يمكن أن يكون المضلع المنتظم

٦) إذا كان قياس الزاوية الخارجة لمضلع منتظم تساوي ٣٠°، ما عدد أضلاع هذا المضلع؟ وما مجموع قياسات زواياه الداخلة؟

عدد الأضلاع = $\frac{\mathrm{٣٦٠}}{\mathrm{٣٠}}$ = ١٢

مجموع قياسات زواياه الداخلة = (١٢ - ٢ × ١٨٠ = ١٨٠٠°

٧) في الشكل المقابل: $\overline{أ ب}$ // $\overline{ء \mathrm{جـ}}$، $\overline{أ \mathrm{جـ}}$ $\cap$ $\overline{ب ء}$ = {م}، ق ($\angle$ ء أ جـ) = ٣٠°، ق ($\angle$ ء ب جـ) = ٤٠°، ق ($\angle$ أ م ب) = ٧٠°

برهن أن الشكل أ ب جـ ء متوازي الأضلاع

م $\in$ أ جـ $\therefore$ ق ($\angle$ ب م جـ) = ١٨٠ - ٧٠ = ١١٠

من $△$ م ب جـ ق ($\angle$ م جـ ب) = ١٨٠ - (٤٠ + ١١٠) = ٣٠°

$\therefore$ ق ($\angle$ أ جـ ب) = ق ($\angle$ ء أ جـ) = ٣٠° وهما متبادلتان.

$\therefore$ أ ء // ب جـ (١) لكن أ ب // ء جـ معطى (٢)

من ١) و٢) الشكل أ ب جـ ء متوازي أضلاع.

٨) في الشكل المقابل: أ ب جـ ء مربع، هـ $\in$ $\underset{ب \mathrm{جـ}}{\leftarrow }$، $\overline{أ \mathrm{جـ}}$ // $\overline{ء \mathrm{هـ}}$

(١) أثبت أن أ جـ هـ ء متوازي الأضلاع

$\because$ أ ب جـ ء مربع $\therefore$ أ ء // ب جـ

$\because$ هـ $\in$ ب جـ $\therefore$ أ ء // جـ هـ (١)

ولكن أ جـ // ء هـ معطى (٢)

من ١) و٢) الشكل أ جـ هـ ء متوازي أضلاع.

(٢) أوجد ق ($\angle$ أ جـ هـ)

$\because$ أ جـ قطر في المربع أ ب جـ ء

$\therefore$ ق ($\angle$ أ جـ ء) = ٤٥°

$\because$ ء جـ $\perp$ ب هـ

$\therefore$ ق ($\angle$ ء جـ هـ) = ٩٠°

$\therefore$ ق ($\angle$ أ جـ هـ) = ٤٥ + ٩٠ = ١٣٥°

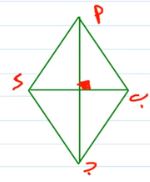
٩) في الشكل المقابل: أ ب جـ ء معين، $\overline{ب ء}$ قطر فيه، ق ($\angle$ أ ب ء) = ٦٢°

أوجد بالبرهان ق ($\angle$ أ)

$\because$ ء ب قطر في المعين أ ب جـ ء

$\therefore$ ق ($\angle$ أ ب ء) = ق ($\angle$ ء ب جـ) = ٦٢

$\therefore$ ق ($\angle$ أ ب جـ) = ٦٢ + ٦٢ = ١٢٤°

ق ($\angle$ أ) = ١٨٠ - ١٢٤ = ٥٦°

١٠) في الشكل المقابل: هـ $\in$ $\overline{ب \mathrm{جـ}}$، ق ($\angle$ ب أ هـ) = ٤٥°، ق ($\angle$ أ هـ ب) = ٧٠°، ق ($\angle$ ء) ٦٥°، ق ($\angle$ جـ) = ١١٥°

برهن أن الشكل أ ب جـ ء متوازي الأضلاع.

في المثلث أ ب هـ ق ($\angle$ ب) = ١٨٠ - (٤٥ + ٧٠) = ٦٥°

مجموع قياسات الزوايا الداخلة للشكل الرباعي = ٣٦٠°

$\therefore$ ق ($\angle$ ب أ ء) = ٣٦٠ - (٦٥ + ١١٥ + ٦٥) = ١١٥°

ق ($\angle$ ب) = ق ($\angle$ ء) (١)

ق ($\angle$ جـ) = ق ($\angle$ ب أ ء) (٢)

من ١) و٢) الشكل أ ب جـ ء متوازي أضلاع.