اختبار الوحدة الثالثة

١) ضع علامة (✔) أمام العبارة الصحيحة وعلامة (×) أمام العبارة غير الصحيحة:

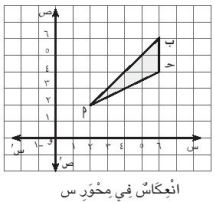
[أ] صورة النقطة (٣، ٤) بانعكاس في محور س هي (٣، -٤).

✔

[ب] النقطة التي صورتها (ص، - س) بدوران حول نقطة الأصل بزاوية قياسها ٩٠° هي (س، ص).

✔

[جـ] صورة النقطة (٥، -٣) بانتقال (س+٢، ص +٤) هي (٧، ١)

✔

[د] في الشكل المقابل:

١) إذا كانت ق $\angle$ هـ ب جـ قائمة فإن $\underset{ب \mathrm{هـ}}{\leftarrow }$ $\perp$ $\overleftrightarrow{أ \mathrm{جـ}}$

✔

٢) إذا كانت ق $\angle$ أ ب هـ قائمة فإن ق ($\angle$ أ ب هـ) = ٩٠°

✔

٣) إذا كان $\underset{ب \mathrm{هـ}}{\leftarrow }$ $\perp$ $\overleftrightarrow{أ \mathrm{جـ}}$ فإن $\angle$ أ ب ء، $\angle$ ء ب هـ متتامتان.

✔

٤) إذا كانت $\angle$ أ ب هـ $\equiv$ $\angle$ حـ ب هـ فإن $\underset{ب \mathrm{هـ}}{\leftarrow }$ $\perp$ $\overleftrightarrow{أ \mathrm{جـ}}$

✔

٢) احسب قياس الزاوية المجهولة في كل مما يأتي:

[أ]

٣س - ٥ = ٧٠

٣س = ١٢٠

س = ٤٠

[ب]

ص = ٦١° بالتناظر.

س = ٦٠°

[جـ]

٣٦ + ٦٤ = ١٠٠

س^٢ = ١٠٠

س = ١٠

[د]

٣س = ٩٠°

س = ٣٠°

٤ص + ٥ص = ١٨٠

٩ص = ١٨٠

ص = ٢٠

[هـ]

٣س - ٨ + س = ١٨٠

٤س - ٨ = ١٨٠°

٤س = ١٨٨

س = ٤٧

[و]

٣ص + ٦ = ٦٠

٣ص = ٥٤

ص = ١٨

٣) [أ] إذا كانت صورة النقطة أ بالانعكاس في محور س هي (٢، ١)، ثم أوجد صورتها بانعكاس في محور ص

أ (٢، -١) الانعكاس على محور الصادات أَ (-٢، -١)

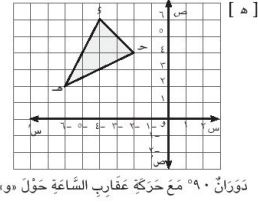
[ب] ارسم المثلث س ص ع الذي فيه س ص = س ع = ٣سم، ص ع = ٤سم، أوجد صورة المثلث س ص ع بدوران حول الرأس س بزاوية قياسها (-٩٠°)

٤) في الأسئلة التالية يرجع إلى الشكل المقابل:

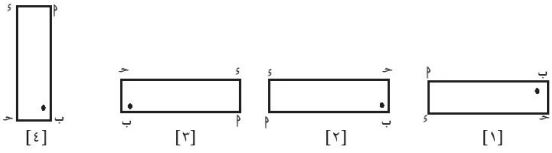
[أ] صورة الشكل بالانعكاس في $\overleftrightarrow{أ ء}$ هي [١، ٢، ٣، ٤]

٢

[ب] صورة الشكل بالدوران حول أ بزاوية قياسها ٩٠° هي [١، ٢، ٣، ٤]

٤

[جـ] صورة الشكل بالانتقال لليمين هي [١، ٢، ٣، ٤]

٣

[د] صورة الشكل بالدوران بزاوية قياسها ١٨٠° حول أ هي [١، ٢، ٣، ٤]

١

٥) في الشكل المقابل: هـ $\in$ $\overline{ب \mathrm{جـ}}$، ق ($\angle$ ب أ هـ) = ٤٥°، ق ($\angle$ أ هـ ب) = ٧٠°، ق ($\angle$ ء) = ٦٥°، ق ($\angle$ جـ) = ١١٥° برهن أن الشكل أ ب جـ ء متوازي الأضلاع.

في المثلث أ ب جـ

ق ($\angle$ ب) = ١٨٠ - ١١٥ = ٦٥°

$\because$ ق ($\angle$ ب هـ جـ) = ١٨٠° لأنها مستقيمة.

ق ($\angle$ أ هـ جـ) = ١٨٠ - ٧٠ = ١١٠°

$\therefore$ ق ($\angle$ هـ أ ء) = ٣٦٠ - (١١٠ + ١١٥ + ٦٥)

= ٧٠°

$\therefore$ ق ($\angle$ أ) = ق ($\angle$ جـ = ١١٥°

ق ($\angle$ ب) = ق ($\angle$ ء) = ٦٥°

إذاً الشكل متوازي أضلاع

٦) [أ] احسب قياس الزاوية المجهولة في كل مما يأتي:

(١)

(٢)

(٣)

[ب] النسبة بين قياسات زوايا الشكل الرباعين هي ٢ : ٣ : ٣ : ٤ أوجد قياس أصغر زاوية

[جـ] عدد أضلاع مضلع ١٥ ضلعاً:

١) أوجد مجموع قياسات زواياه الداخلة.

٢) إذا كان مجموع قياسات خمسة من زواياه الخارجة يساوي ٢٠٠°، أوجد مجموع قياسات الزوايا العشرة الداخلة غير المجاورة للزوايا الخمسة الخارجة.

٧) في الشكل المقابل: ء منتصف $\overline{أ ب}$، هـ منتصف $\overline{أ \mathrm{جـ}}$، $\overline{ء و}$ $\cap$ $\overline{ب \mathrm{جـ}}$ = {س}، ء س = س و، ب جـ = ١٢ سم. أوجد طول $\overline{س ص}$

بما أن ء، هـ منتصف $\overline{أ ب}$، $\overline{أ \mathrm{جـ}}$

ء هـ = $\frac{\mathrm{١}}{\mathrm{٢}}$ $\overline{ب \mathrm{جـ}}$، $\overline{ء \mathrm{هـ}}$ // $\overline{ب \mathrm{جـ}}$

ء هـ = ٦سم

في المثلث ء هـ و بما أن س منتصف $\overline{ء و}$

$\overline{ء \mathrm{هـ}}$ // $\overline{س ص}$

إذا ص منتصف $\overline{و \mathrm{هـ}}$

إذاً س ص = $\frac{\mathrm{١}}{\mathrm{٢}}$ $\overline{ء \mathrm{هـ}}$ = ٣سم.

٨) انقل كل شكل مما يأتي على ورق مربعات، ارسم صورة الأشكال بتحويل هندسي كما هو موضح أسفل كل شكل تم اكتب إحداثي كل رأس من رؤوس الشكل:

أ)

ب)

جـ)

هـ)

د)

و)