الدرس التاسع: الانتقال في المستوى الإحداثي

١) أوجد صورة متوازي الأضلاع أ ب جـ ء المرسوم على الشبكة التربيعية بالانتقال التالي:

[أ] (س، ص) $\leftarrow$ (س + ٥، ص + ٢)

[ب] (س، ص) $\leftarrow$ (س -٨، ص -١)

[جـ] (س، ص) $\leftarrow$ (س + ٢، ص -٤)

[د] (س، ص) $\leftarrow$ (س -٤، ص + ٢)

٢) باستخدام شبكة تربيعية أوجد صورة كل مما يأتي بانتقال ل م في اتجاه $\underset{ل م}{\leftarrow }$، حيث ل (١، ٣)، م (٤، ٥)

قاعدة الانتقال = (٤ -١، ٥ - ٣) = (٣، ٢)

[أ] (-٢، ٣)

[ب] (٥، ٤)

[جـ] (٣، ٠)

أَ = (-٢ +٣، ٣ + ٢) = (١، ٥)

بَ = (٥ + ٣، ٤ + ٢) = (٨، ٦)

جـَ = (٣ + ٣، ٢ + ٠) = (٦، ٢)

٣) بتطبيق الانتقال الذي يحول النقطة (س، ص) إلى النقطة (س + ٢، ص + ٣) أوجد النقطة التي صورتها (٢، ٣)

(٢ -٢، ٣ -٣) = (٠، ٠)

النقطة (٠، ٠)

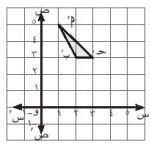
٤) في الشكل المقابل: إذا كان $△$ اَ بَ جـَ هو صورة $△$ أ ب جـ بانتقال: (س، ص) $\leftarrow$ (س + ٢، ص + ٣)، ارسم $△$ أ ب جـ ثم أوجد إحداثيات رؤوس $△$ أ ب جـ

أَ (١، ٥) $\leftarrow$ أ (١ -٢، ٥ - ٣) = (-١، ٢)

بَ (٢، ٣) $\leftarrow$ ب (٢ -٢، ٣ -٣) = (٠، ٠)

جـَ (٣، ٣) $\leftarrow$ جـ (٣-٢، ٣ -٣) = (١، ٠)

٥) إذا كانت صورة النقطة أ (١، ١) بالانتقال في المستوى هي أَ (٢، ٢) أوجد صورة النقط التالية بنفس الانتقال: و (٠، ٠)، ب (-١، ٣)، جـ (-٣، ٥)

الانتقال = (٢-١، ٢-١) = (١، ١)

و (٠، ٠) $\leftarrow$ (٠ +١، ٠ +١) = (١، ١)

ب (-١، ٣) $\leftarrow$ (-١+١، ٣+١) = (٠، ٤)

جـ (-٣، ٥) $\leftarrow$ (-٣+١، ٥ +١) = (-٢، ٦)

٦) إذا كان إحداثيات رؤوس المربع أ ب جـ ء هي: أ (١، ١)، ب (٤، ٢)، جـ (٣، ٥)، ء (٠، ٤)

[أ] ارسم المربع وصورته بانتقال أ ب في اتجاه $\underset{أ ب}{\leftarrow }$

[ب] اكتب قاعدة الانتقال.

قاعدة الانتقال = (٤ -١، ٢ -١) = (٣، ١)

أ = (١، ١) $\leftarrow$ أَ = (٤، ٢)

ب = (٤، ٢) $\leftarrow$ بَ = (٧، ٣)

جـ = (٣، ٥) $\leftarrow$ جـَ = (٦، ٦)

ء = (٠، ٤) $\leftarrow$ ءَ = (٣، ٥)

٧) النقطة أَ (٣، -٣) هي صورة النقطة أ بانتقال قاعدته: (س، ص) $\leftarrow$ (س -١، ص - ٤) ارسم النقطة أ وصورتها أَ على الشبكة التربيعية وبنفس الانتقال أوجد صورة المثلث أ ب جـ حيث ب (٥، ٠)، جـ (-١، -٢)

أ = (٣ +١، -٣+٤) = (٤، ١)

بَ = (٥ -١، ٠-٤) = (٤، -٤)

جـَ = (-١-١، -٢-٤) = (-٢، -٦)